MAProcess

MAProcess[{b1,…,bq},v]

represents a moving-average process of order q with normal white noise variance v.

MAProcess[{b1,…,bq},Σ]

represents a vector MA process with multinormal white noise covariance matrix Σ.

MAProcess[{b1,…,bq},v,init]

represents an MA process with initial data init.

MAProcess[c,…]

represents an MA process with a constant c.

Details

  • MAProcess is also known as a finite impulse response (FIR) filter.
  • MAProcess is a discrete-time and continuous-state random process.
  • The MA process is described by the difference equation 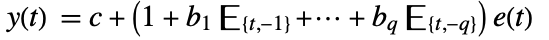, where 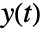is the state output, 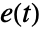is white noise input, 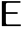is the shift operator, and the constant c is taken to be zero if not specified.
  • The initial data init can be given as a list {…,y[-2],y[-1]} or a single-path TemporalData object with time stamps understood as {…,-2,-1}.
  • A scalar MA process should have real coefficients bi and c, and a positive variance v.
  • An 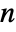-dimensional vector MA process should have real coefficient matrices bi of dimensions 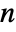×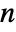, real vector c of length 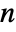, and the covariance matrix Σ should be symmetric positive definite of dimensions ×.
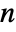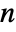  • The MA process with zero constant has transfer function 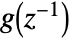where:
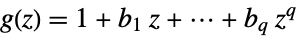
  • scalar process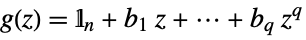
    vector process; 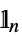is the 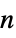× 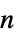identity matrix
  • MAProcess[tproc,q] for a time series process tproc gives an MA process of order q such that the series expansions about zero of the corresponding transfer functions agree up to degree q.
  • Possible time series processes tproc include ARProcess, ARMAProcess, and SARIMAProcess.
  • MAProcess[q] represents a moving-average process of order q for use in EstimatedProcess and related functions.
  • MAProcess can be used with such functions as CovarianceFunction, RandomFunction, and TimeSeriesForecast.

Examples

open allclose all

Basic Examples  (3)

Simulate an MA process:

Covariance function:

Correlation function:

Partial correlation function:

Scope  (37)

Basic Uses  (11)

Simulate an ensemble of paths:

Simulate with given precision:

Simulate a first-order scalar process:

Sample paths for positive and negative values of the parameter:

Initial values do not influence the process values:

Simulate a two-dimensional process:

Create a 2D sample path function from the data:

The color of the path is the function of time:

Create a 3D sample path function with time:

The color of the path is the function of time:

Simulate a three-dimensional process:

Create a sample path function from the data:

The color of the path is the function of time:

Estimation:

Compare the sample covariance functions with the one of the estimated process:

Use TimeSeriesModel to automatically find orders:

Compare the sample covariance functions with the best time series model:

Find maximum likelihood estimator:

Fix the constant and the variance and estimate the remaining parameters:

Plot the log-likelihood function together with the position of the estimated parameters:

Estimate a vector moving-average process:

Compare covariance functions for each component:

Forecast future values:

Show the forecast path:

Plot the data and the forecasted values:

Find a forecast for a vector-valued time series process:

Find the forecast for the next 10 steps:

Plot the data and the forecast for each component:

Covariance and Spectrum  (6)

Correlation function exists in closed form:

Closed form of the partial correlation function for the first order:

Covariance matrix:

Covariance matrix of an MAProcess is symmetric multidiagonal:

Correlation matrix:

Covariance function for a vector-valued process:

Power spectral density:

Vector MAProcess:

Stationarity and Invertibility  (4)

MAProcess is weakly stationary for any choice of parameters:

For a vector process:

Check if a time series is invertible:

For a vector process:

Find invertible representation for a moving-average process:

The moments are being conserved:

Find invertibility conditions:

Find conditions for higher order:

Estimation Methods  (6)

The available methods for estimating an MAProcess:

Compare log likelihoods:

Method of moments allows following solvers:

This method allows for fixed parameters:

Some relations between parameters are also permitted:

Maximum conditional likelihood method allows following solvers:

This method allows for fixed parameters:

Some relations between parameters are also permitted:

Maximum likelihood method allows following solvers:

This method allows for fixed parameters:

Some relations between parameters are also permitted:

Spectral estimator allows to specify windows used for PowerSpectralDensity calculation:

Spectral estimator allows following solvers:

This method allows for fixed parameters:

Some relations between parameters are also permitted:

Minimum prediction method:

This method allows for fixed parameters:

Process Slice Properties  (5)

Single time SliceDistribution:

Multiple time slice distributions:

Slice distribution of a vector-valued time series:

First-order probability density function:

Stationary mean and variance:

Compare with the density function of a normal distribution:

Compute the expectation of an expression:

Calculate a probability:

Skewness and kurtosis are constant:

Moment of order r:

Generating functions:

CentralMoment and its generating function:

FactorialMoment has no closed form for symbolic order:

Cumulant and its generating function:

Representations  (5)

Approximate an AR process with an MA process of order 5:

Compare the covariance function for the original and the approximate processes:

Approximate a vector process:

Approximate an ARMA process with an MA process:

Compare sample paths:

Approximate a SARIMA process with an MA process:

Compare sample paths:

TransferFunctionModel representation:

For a vector-valued process:

StateSpaceModel representation:

For a vector-valued process:

Applications  (1)

Consider the following time series data and determine whether it is adequately modeled by an MAProcess:

The correlation function drops off after lag 3. This is evidence of an MAProcess[3]:

The partial correlation alternates and dampens slowly, which also indicates an MAProcess:

Fit an MAProcess[3] model to the data:

Find residuals between the data and the model:

Test if residuals are normal white noise:

Properties & Relations  (5)

MAProcess is a special case of an ARMAProcess:

MAProcess is a special case of an ARIMAProcess:

MAProcess is a special case of a FARIMAProcess:

MAProcess is a special case of a SARMAProcess:

MAProcess is a special case of a SARIMAProcess:

Possible Issues  (3)

ToInvertibleTimeSeries does not always exist:

There are zeros of the TransferFunctionModel on the unit circle:

The method of moments may not find a solution in estimation:

Use a different solver:

Minimum prediction error estimation method does not allow repeated parameters:

Use a different method:

Neat Examples  (2)

Simulate a three-dimensional MAProcess:

Simulate paths from an MA process:

Take a slice at 50 and visualize its distribution:

Plot paths and histogram distribution of the slice distribution at 50:

Wolfram Research (2012), MAProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/MAProcess.html (updated 2014).

Text

Wolfram Research (2012), MAProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/MAProcess.html (updated 2014).

CMS

Wolfram Language. 2012. "MAProcess." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/MAProcess.html.

APA

Wolfram Language. (2012). MAProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MAProcess.html

BibTeX

@misc{reference.wolfram_2024_maprocess, author="Wolfram Research", title="{MAProcess}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MAProcess.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_maprocess, organization={Wolfram Research}, title={MAProcess}, year={2014}, url={https://reference.wolfram.com/language/ref/MAProcess.html}, note=[Accessed: 22-November-2024 ]}