CovarianceEstimatorFunction
is an option for generalized linear model fitting functions that specifies the estimator for the parameter covariance matrix.
Details
- CovarianceEstimatorFunction is an option for GeneralizedLinearModelFit, LogitModelFit, and ProbitModelFit.
- Possible settings include "ExpectedInformation" and "ObservedInformation" which use the expected information matrix and observed information matrix, respectively.
- The covariance matrix is equivalent to
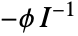, where ϕ is the dispersion parameter and 
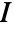is Fisher's information matrix.
Examples
open all close allBasic Examples (1)
Scope (2)
Specify the covariance estimate within the FittedModel:
Use with LogitModelFit:
Use with ProbitModelFit:
Properties & Relations (2)
Error estimates and confidence intervals involve covariance estimates:
Estimate errors and intervals using expected information:
CovarianceEstimatorFunction controls the general structure of the covariance:
DispersionEstimatorFunction affects the scale:
The ratio of the errors squared is the ratio of the dispersion estimates:
Text
Wolfram Research (2008), CovarianceEstimatorFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/CovarianceEstimatorFunction.html.
CMS
Wolfram Language. 2008. "CovarianceEstimatorFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CovarianceEstimatorFunction.html.
APA
Wolfram Language. (2008). CovarianceEstimatorFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CovarianceEstimatorFunction.html