DedekindEta

DedekindEta[τ]

デデキント(Dedekind)イータ・モジュラ法楕円関数 TemplateBox[{tau}, DedekindEta]を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • DedekindEtaは，複素 τ 平面の上半面上に定義される．実数 τ に対しては定義されない．
  • 引数 τ は，ワイエルシュトラス(Weierstrass)の半周期 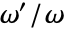の比である．
  • DedekindEtaは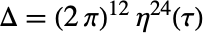を満足させる．この際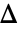，は判別式であり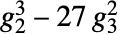，によってワイエルシュトラスの不変元として与えられる．
  • 特別な引数の場合，DedekindEtaは，自動的に厳密値を計算する．
  • DedekindEtaは任意の数値精度で評価できる．
  • DedekindEtaは自動的にリストに縫い込まれる．
  • DedekindEtaはCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例  (2)

数値的に評価する：

実数の部分集合上でプロットする：

スコープ  (14)

数値評価  (4)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

高精度で効率的に評価する：

DedekindEtaはCenteredIntervalオブジェクトに使うことができる：

特定の値  (2)

固定点における値：

DedekindEtaは要素単位でリストに縫い込まれる：

可視化  (2)

DedekindEta関数をさまざまなパラメータについてプロットする：

DedekindEta関数の実部を三次元でプロットする：

DedekindEta関数の虚部を三次元でプロットする：

関数の特性  (6)

DedekindEtaの複素領域：

DedekindEtaは周期関数である：

DedekindEtaはその定義域において解析関数である：

しかし，整関数ではない：

特異点と不連続点の両方を持つ：

DedekindEtaは複素数上で単射である：

DedekindEtaは全射ではない：

TraditionalFormによる表示：

アプリケーション  (3)

Iにおけるモジュラー判別式はDedekindEtaによって与えられる：

一般的な定義と比較する：

複素平面の上半分でDedekindEta関数をプロットする：

モジュール判別式：

DedekindEtaとの関係：

特性と関係  (2)

機械精度の入力では正しい答を得るのには不十分である：

厳密な入力を与えると正しい答が返される：

DedekindEtaは数値引数を持つ数値関数なので数量と考えられるかもしれないが，その分析性の境界により，数値に評価されないこともある：

Wolfram Research (1996), DedekindEta, Wolfram言語関数， https://reference.wolfram.com/language/ref/DedekindEta.html （2021年に更新）.

テキスト

Wolfram Research (1996), DedekindEta, Wolfram言語関数， https://reference.wolfram.com/language/ref/DedekindEta.html （2021年に更新）.

CMS

Wolfram Language. 1996. "DedekindEta." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/DedekindEta.html.

APA

Wolfram Language. (1996). DedekindEta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DedekindEta.html

BibTeX

@misc{reference.wolfram_2024_dedekindeta, author="Wolfram Research", title="{DedekindEta}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/DedekindEta.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_dedekindeta, organization={Wolfram Research}, title={DedekindEta}, year={2021}, url={https://reference.wolfram.com/language/ref/DedekindEta.html}, note=[Accessed: 22-November-2024 ]}