gives the modular lambda elliptic function ![]() .
.


ModularLambda
gives the modular lambda elliptic function ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- ModularLambda is defined only in the upper half of the complex
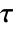 plane. It is not defined for real
plane. It is not defined for real 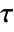 .
. - The argument
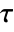 is the ratio of Weierstrass half‐periods
is the ratio of Weierstrass half‐periods 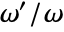 .
. - ModularLambda gives the parameter
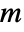 for elliptic functions in terms of
for elliptic functions in terms of 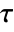 according to
according to ![m=TemplateBox[{tau}, ModularLambda] m=TemplateBox[{tau}, ModularLambda]](Files/ModularLambda.en/8.png) .
. - ModularLambda is related to EllipticTheta by
![TemplateBox[{tau}, ModularLambda]=TemplateBox[{2, 0, q}, EllipticTheta]^4/TemplateBox[{3, 0, q}, EllipticTheta]^4 TemplateBox[{tau}, ModularLambda]=TemplateBox[{2, 0, q}, EllipticTheta]^4/TemplateBox[{3, 0, q}, EllipticTheta]^4](Files/ModularLambda.en/9.png) where the nome
where the nome 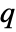 is given by
is given by 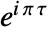 .
. 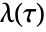 is invariant under any combination of the modular transformations
is invariant under any combination of the modular transformations 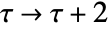 and
and 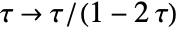 . »
. »- For certain special arguments, ModularLambda automatically evaluates to exact values.
- ModularLambda can be evaluated to arbitrary numerical precision.
- ModularLambda can be used with CenteredInterval objects. »
- ModularLambda automatically threads over lists. »
Examples
open all close allBasic Examples (3)
Scope (23)
Numerical Evaluation (5)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
Compute the elementwise values of an array using automatic threading:
Or compute the matrix ModularLambda function using MatrixFunction:
ModularLambda can be used with CenteredInterval objects:
Specific Values (2)
Visualization (3)
Plot the real part of ModularLambda:
Plot the absolute value of ModularLambda:
Plot the real part of ModularLambda function:
Plot the imaginary part of ModularLambda function:
Function Properties (9)
ModularLambda is defined in the upper half-plane:
ModularLambda is a periodic function:
ModularLambda threads elementwise over lists:
ModularLambda is an analytic function on its domain:
Therefore it has neither singularities nor discontinuities there:
![]() is neither nondecreasing nor nonincreasing:
is neither nondecreasing nor nonincreasing:
![]() is neither non-negative nor non-positive:
is neither non-negative nor non-positive:
![]() is neither convex nor concave:
is neither convex nor concave:
TraditionalForm formatting:
Differentiation (2)
Series Expansions (2)
Find the Taylor expansion using Series:
Applications (4)
Some modular properties of ModularLambda are automatically applied:
Verify a more complicated identity numerically:
ModularLambda is a modular function. Make an ansatz for a modular equation:
Form an overdetermined system of equations and solve it:
This is the modular equation of order 2:
Possible Issues (2)
Machine-precision input is insufficient to give a correct answer:
With exact input, the answer is correct:
ModularLambda remains unevaluated outside of its domain of analyticity:
Tech Notes
Related Guides
Related Links
History
Introduced in 1996 (3.0) | Updated in 2021 (13.0)
Text
Wolfram Research (1996), ModularLambda, Wolfram Language function, https://reference.wolfram.com/language/ref/ModularLambda.html (updated 2021).
CMS
Wolfram Language. 1996. "ModularLambda." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ModularLambda.html.
APA
Wolfram Language. (1996). ModularLambda. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ModularLambda.html
BibTeX
@misc{reference.wolfram_2025_modularlambda, author="Wolfram Research", title="{ModularLambda}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/ModularLambda.html}", note=[Accessed: 12-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_modularlambda, organization={Wolfram Research}, title={ModularLambda}, year={2021}, url={https://reference.wolfram.com/language/ref/ModularLambda.html}, note=[Accessed: 12-March-2026]}