DiscreteLQEstimatorGains

DiscreteLQEstimatorGains[ssm,{w,v},τ]

gives the optimal discrete-time estimator gain matrix with sampling period τ for the continuous-time StateSpaceModel ssm, with process and measurement noise covariance matrices w and v.

DiscreteLQEstimatorGains[{ssm,sensors},{w,v},τ]

specifies sensors as the noisy measurements of ssm.

DiscreteLQEstimatorGains[{ssm,sensors,dinputs},{w,v},τ]

specifies dinputs as the deterministic inputs of ssm.

Details and Options

  • The standard state-space model ssm can be given as StateSpaceModel[{a,b,c,d}], where a, b, c, and d represent the state, input, output, and transmission matrices of the continuous-time system .
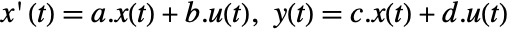  • The descriptor continuous-time state-space model ssm defined by 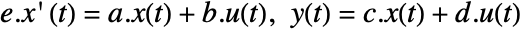can be given as StateSpaceModel[{a,b,c,d,e}].
  • The input 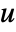can include the process noise 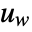, as well as deterministic inputs .
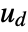  • The argument dinputs is a list of integers specifying the positions of 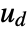in .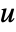
  • The output 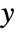consists of the noisy measurements 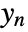, as well as other outputs.
  • The argument sensors is a list of integers specifying the positions of 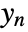in .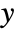
  • DiscreteLQEstimatorGains[ssm,{…},τ] is equivalent to DiscreteLQEstimatorGains[{ssm, All,None},{…},τ].
  • The noisy measurements are modeled as 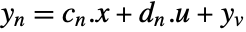, where 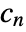and 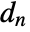are the submatrices of 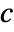and 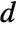associated with 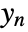, and 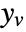is the noise.
  • The process and measurement noises are assumed to be white and Gaussian:
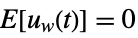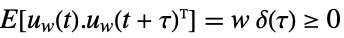
  • , process noise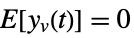
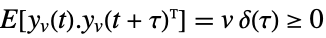
    , measurement noise
  • The estimator with the optimal gain minimizes 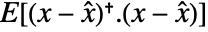, where 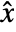is the estimated state vector.
  • DiscreteLQEstimatorGains computes the estimator gains based on the discrete equivalent of the noise matrices.
  • The state-space model ssm is discretized using the zero-order hold method.

Examples

open allclose all

Basic Examples  (1)

Compute the discrete LQ estimator gains for a continuous-time state-space model:

Scope  (3)

Compute the discrete-time Kalman gains for a state-space model:

The gains based on the measurement of just the second output:

The gains for a system in which all inputs except the first are stochastic:

Find the optimal gains for a descriptor state-space model:

Properties & Relations  (1)

Find estimator gains using DiscreteLQEstimatorGains:

Create a discrete-time Kalman estimator with the gains and a discretized model:

This is different from that obtained by discretizing a continuous-time estimator:

Response of the first estimator in the presence of process and measurement noises:

Response of the discretized Kalman estimator:

The responses are different:

Possible Issues  (1)

The system must be detectable:

Wolfram Research (2010), DiscreteLQEstimatorGains, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteLQEstimatorGains.html (updated 2012).

Text

Wolfram Research (2010), DiscreteLQEstimatorGains, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteLQEstimatorGains.html (updated 2012).

CMS

Wolfram Language. 2010. "DiscreteLQEstimatorGains." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/DiscreteLQEstimatorGains.html.

APA

Wolfram Language. (2010). DiscreteLQEstimatorGains. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteLQEstimatorGains.html

BibTeX

@misc{reference.wolfram_2024_discretelqestimatorgains, author="Wolfram Research", title="{DiscreteLQEstimatorGains}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteLQEstimatorGains.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_discretelqestimatorgains, organization={Wolfram Research}, title={DiscreteLQEstimatorGains}, year={2012}, url={https://reference.wolfram.com/language/ref/DiscreteLQEstimatorGains.html}, note=[Accessed: 21-December-2024 ]}