DivisorSigma[k,n]
gives the divisor function ![]() .
.


DivisorSigma
DivisorSigma[k,n]
gives the divisor function ![]() .
.
Details and Options

- DivisorSigma is also known as the divisor function or sum‐of‐divisors function.
- Integer mathematical function, suitable for both symbolic and numerical manipulation.
- DivisorSigma[k,n] is the sum of the k
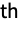 powers of the divisors of n.
powers of the divisors of n. - For a number
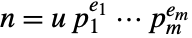 with
with 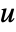 a unit and
a unit and 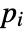 primes, DivisorSigma[k,n] returns
primes, DivisorSigma[k,n] returns 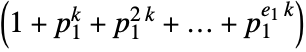
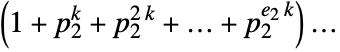 .
. - With the setting GaussianIntegers->True, DivisorSigma includes divisors that are Gaussian integers.
- DivisorSigma[k,m+In] automatically works over Gaussian integers.
Examples
open all close allBasic Examples (2)
The sum of squares of divisors:
Plot DivisorSigma with log-scaled values:
Scope (12)
Numerical Evaluation (4)
DivisorSigma works over integers:
DivisorSigma threads elementwise over lists:
Symbolic Manipulation (8)
Applications (13)
Basic Applications (3)
In general, DivisorSigma[d,n]=∑k|nkd:
The ratio of Gaussian divisors to integer divisors:
Plot DivisorSigma with log-scaled values:
Special Sequences (4)
Recognize perfect numbers, numbers n such that the sum of their divisors is equal to ![]() :
:
Deficient numbers, numbers n such that the sum of their divisors is smaller than ![]() :
:
Abundant numbers, numbers n such that the sum of their divisors is greater than ![]() :
:
Recognize highly composite numbers: [more info]
Recognize amicable numbers, two different numbers such that the sum of the proper divisors of each is equal to the other number:
Recognize ![]() -multiperfect numbers, numbers such that the sum of their divisors is equal to
-multiperfect numbers, numbers such that the sum of their divisors is equal to ![]() :
:
Number Theory (6)
If n is a power of ![]() , then the sum of the divisors of n equals
, then the sum of the divisors of n equals ![]() , which makes n almost perfect:
, which makes n almost perfect:
The number of the divisors is odd if and only if the number is a perfect square:
Compare the number of divisors with Euler's totient function:
Plot the running average of the number of divisors with its asymptotic value:
Properties & Relations (6)
DivisorSigma is the sum of the ![]() powers of the divisors:
powers of the divisors:
Use DivisorSum to find the sum of divisors:
DivisorSigma is a multiplicative function:
The reciprocals of the divisors of a perfect number n must add up to ![]() :
:
The sum of divisors of a prime power n is less than 2n:
For a prime number p, the number of the divisors is ![]() :
:
The number of divisors of ![]() is
is ![]() :
:
Use DivisorSigma to find the product of divisors:
Possible Issues (1)
With GaussianIntegers->True, the naive definition does not give the correct result:
To make DivisorSigma a multiplicative function, a definition involving factors is used:
Neat Examples (4)
Plot the arguments of the Fourier transform of DivisorSigma:
Plot the absolute values of the Fourier transform of DivisorSigma:
Plot the arguments of the Fourier transform of DivisorSigma:
Tech Notes
Related Links
History
Introduced in 1988 (1.0)
Text
Wolfram Research (1988), DivisorSigma, Wolfram Language function, https://reference.wolfram.com/language/ref/DivisorSigma.html.
CMS
Wolfram Language. 1988. "DivisorSigma." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DivisorSigma.html.
APA
Wolfram Language. (1988). DivisorSigma. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DivisorSigma.html
BibTeX
@misc{reference.wolfram_2025_divisorsigma, author="Wolfram Research", title="{DivisorSigma}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/DivisorSigma.html}", note=[Accessed: 12-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_divisorsigma, organization={Wolfram Research}, title={DivisorSigma}, year={1988}, url={https://reference.wolfram.com/language/ref/DivisorSigma.html}, note=[Accessed: 12-March-2026]}