E

E

表示数值 的指数常数 （自然对数的底）.

更多信息

背景

  • E 这一符号表示的是自然对数 Log 的底数. 它也被称为欧拉数，可用 \[ExponentialE]输入. E 在数学中有很多等价定义，包括非负整数阶乘倒数的无穷和 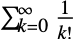以及 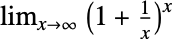的极限值. 它的数值 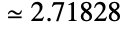. E 可能是数学中除了 Pi 之外最重要的常数. 它出现在许多求和，求积，积分，复利方程，指数增长或衰减的规律，以及其它广泛的数学和科学领域中的公式中.
  • 指数函数 Exp[x] 可以写成 E^x. 当 E 作为符号时，它被当成精确值参与计算. 对包含 E 的表达式的展开和化简需要诸如 FunctionExpand 和 FullSimplify 这样的函数.
  • 欧拉证明了 E 是无理数（这意味着它不能被表示为任何两个整数的比值）而埃尔米特随后证明了它是超越数（这意味着它不是任何整系数多项式的根）. 然而，E 可能是“最小”的的超越数因为它的无理性测度是 2. 目前我们不知道 E 是否是某个进制下的正规数（这意味着它在 b 进制下展开的各位数字是均匀分布的）. 除了广泛的出现在各种闭形式的求和与积分中之外，有猜想认为 E 不是一个 Kontsevich–Zagier 节（这意味着它不是任何 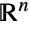中的代数整环上的有理系数单元或多元有理函数的绝对收敛积分值）.
  • 可以用 N 算出 E 的任意精度的数值. 事实上在一台现代台式电脑上计算 E 的前一百万位数字耗时都不到一秒. RealDigits 可用于返回 E 的各位数字列表而 ContinuedFraction 则可得到其连分数展开的各项.

范例

打开所有单元关闭所有单元

基本范例  (3)

E 可以用 ee 来输入(对于“指数 e”)：

计算任意精度：

执行一个精确数值计算：

应用  (5)

以 10 为底的 的前 20 位数字：

有一个正则连分数：

计算与 相关的符号关系：

数学函数和操作通常给出与 相关的结果：

解决 Steiner 问题：

属性和关系  (5)

Exp[z] 自动转换到 z：

不是一个代数数：

用 TrigToExp 从双曲线函数和三角函数中获得 E：

求以10 为底，百万分之一之后的前 20 个数字：

许多极限结果中的 级数：

巧妙范例  (1)

与 E 相关的韦尔（Weyl）型的和：

Wolfram Research (1988)，E，Wolfram 语言函数，https://reference.wolfram.com/language/ref/E.html （更新于 2002 年）.

文本

Wolfram Research (1988)，E，Wolfram 语言函数，https://reference.wolfram.com/language/ref/E.html （更新于 2002 年）.

CMS

Wolfram 语言. 1988. "E." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2002. https://reference.wolfram.com/language/ref/E.html.

APA

Wolfram 语言. (1988). E. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/E.html 年

BibTeX

@misc{reference.wolfram_2024_e, author="Wolfram Research", title="{E}", year="2002", howpublished="\url{https://reference.wolfram.com/language/ref/E.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_e, organization={Wolfram Research}, title={E}, year={2002}, url={https://reference.wolfram.com/language/ref/E.html}, note=[Accessed: 22-November-2024 ]}