ElectricCurrentPDEComponent
ElectricCurrentPDEComponent[vars,pars]
生成带有变量 vars 和参数 pars 的电流偏微分方程项.
更多信息



- ElectricCurrentPDEComponent 通常用于生成具有模型变量 vars 和模型参数 pars 的电流连续性方程.
- ElectricCurrentPDEComponent 返回一组微分算子之和,用作偏微分方程的一部分:
- ElectricCurrentPDEComponent 创建用于稳态、频率和参数分析的偏微分方程项.
- ElectricCurrentPDEComponent 模拟导电材料中由直流或交流电流产生的电场,在此情况下可忽略磁效应和感应效应.
- ElectricCurrentPDEComponent 的结果可用于计算电流密度的大小. »
- ElectricCurrentPDEComponent 模拟稳态或谐波电场,其中电标量电势
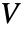 [
[![TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/4.png) ] 为因变量,
] 为因变量, 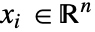 [
[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/6.png) ] 为自变量.
] 为自变量. - 稳态变量 vars 为 vars={V[x1,…,xn],{x1,…,xn}}.
- 与频率相关的变量 vars 为 vars={V[x1,…,xn],ω,{x1,…,xn}}.
- 电流连续性方程为
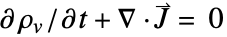 ,其中体电荷密度
,其中体电荷密度 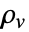 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 3}}, coulombs per meter cubed, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 3}}, coulombs per meter cubed, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/9.png) ],时间变量
],时间变量 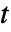 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/11.png) ],电流密度向量
],电流密度向量 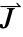 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/13.png) ].
]. - 本构材料模型方程,即欧姆定律,为
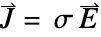 ,其中
,其中 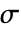 [
[![TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/16.png) ] 为导电率,
] 为导电率,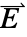 [
[![TemplateBox[{InterpretationBox[, 1], {"V", , "/", , "m"}, volts per meter, {{(, "Volts", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"V", , "/", , "m"}, volts per meter, {{(, "Volts", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/18.png) ] 为电场强度,且有
] 为电场强度,且有 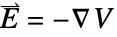 .
. - ElectricCurrentPDEComponent 提供了一个稳态电流模型:
- 其中
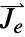 是一个外部产生的电流密度矢量, 单位为 [
是一个外部产生的电流密度矢量, 单位为 [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/22.png) ],
],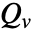 代表电流源,单位为 [
代表电流源,单位为 [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 3}}, amperes per meter cubed, {{(, "Amperes", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 3}}, amperes per meter cubed, {{(, "Amperes", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/24.png) ].
]. - ElectricCurrentPDEComponent 提供了一个频率域模型:
- 其中真空介电常数
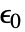 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/27.png) ],极化矢量
],极化矢量 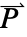 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/29.png) ],角频率
],角频率 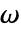 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/31.png) ],虚数单位为
],虚数单位为 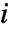 .
. - 对于线性材料,频率域模型可以简化为:
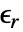 是无量纲的相对介电常数.
是无量纲的相对介电常数.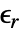 可以是各向同性、正交各向异性,或完全各向异性.
可以是各向同性、正交各向异性,或完全各向异性.- 对于电流模型,隐含的默认边界条件是 0 ElectricCurrentDensityValue.
- 电流模型中各项的单位是 [
![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 3}}, amperes per meter cubed, {{(, "Amperes", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 3}}, amperes per meter cubed, {{(, "Amperes", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/36.png) ].
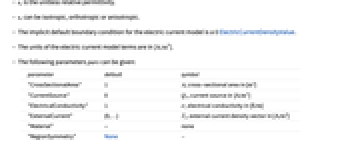
]. - 可以给出以下参数 pars:
-
参数 默认值 符号 "CrossSectionalArea" 1 横截面积 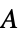 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {{"m", ^, 2}}, meters squared, {"Meters", ^, 2}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {{"m", ^, 2}}, meters squared, {"Meters", ^, 2}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/38.png) ]
] "CurrentSource" 0 电流源 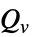 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 3}}, amperes per meter cubed, {{(, "Amperes", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 3}}, amperes per meter cubed, {{(, "Amperes", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/40.png) ]
]"ElectricalConductivity" 1 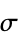 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/42.png) ]
]
"ExternalCurrentSource" {0,…} 外部电流密度矢量 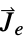 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/44.png) ]
]"Material" - 无 "RegionSymmetry" None 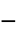
"Thickness" 1 厚度 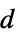 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/47.png) ]
] - 如果指定了 "Material",则相关的材料常数将从材料数据中提取;否则,需要明确指定相关的材料参数.
- 对于频域模型,可以指定额外的参数:
-
参数 默认值 符号 "Polarization" {0,…} 极化矢量 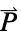 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/49.png) ]
]"RelativePermittivity" 1 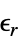 ,无量纲的相对介电常数
,无量纲的相对介电常数
"RemanentPolarization" {0,…} 残余极化矢量 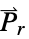 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/52.png) ]
]"VacuumPermittivity" 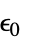
真空介电常数 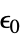 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.zh/55.png) ]
] - 所有参数可能取决于空间变量
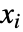 和因变量
和因变量 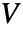 .
. - 自变量
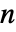 的数量决定了
的数量决定了 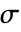 、
、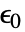 和
和 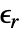 的维度,以及矢量
的维度,以及矢量 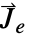 、
、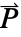 和
和 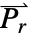 的长度.
的长度. - 参数 "RegionSymmetry" 的可能选择是 "Axisymmetric".
- "Axisymmetric" 区域对称性表示一个截断的柱坐标系,其中柱坐标通过移除角变量被简化,具体如下:
-
维度 简化 例如:稳态方程 1D 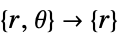
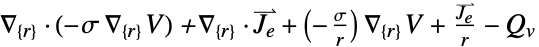
2D 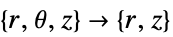
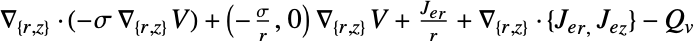
- 在一维情况下,如果指定了 "CrossSectionalArea"
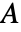 ,ElectricCurrentPDEComponent 方程如下:
,ElectricCurrentPDEComponent 方程如下: - 在一维情况下,如果指定了 "Thickness"
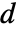 ,ElectricCurrentPDEComponent 方程如下:
,ElectricCurrentPDEComponent 方程如下: - 在一维轴对称情况下,当指定 "Thickness"
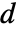 时,ElectricCurrentPDEComponent 方程如下:
时,ElectricCurrentPDEComponent 方程如下: - 参数的输入规范与其相应的运算符项完全相同.
- 如果不指定参数,则默认电流偏微分方程为:
- 如果 ElectricCurrentPDEComponent 取决于在关联 pars 中指定为 …,keypi…,pivi,…] 的参数
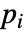 ,则参数
,则参数 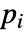 将替换为
将替换为 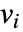 .
.
范例
打开所有单元关闭所有单元范围 (6)
指定一个稳态电流的偏微分方程,其中电导率 ![]() (单位为 [
(单位为 [![]() ]),外部电流密度
]),外部电流密度 ![]() (单位为[
(单位为[![]() ]):
]):
用 Activate 激活一个特定材料的稳态电流偏微分方程模型:
Wolfram Research (2024),ElectricCurrentPDEComponent,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ElectricCurrentPDEComponent.html (更新于 2025 年).
文本
Wolfram Research (2024),ElectricCurrentPDEComponent,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ElectricCurrentPDEComponent.html (更新于 2025 年).
CMS
Wolfram 语言. 2024. "ElectricCurrentPDEComponent." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2025. https://reference.wolfram.com/language/ref/ElectricCurrentPDEComponent.html.
APA
Wolfram 语言. (2024). ElectricCurrentPDEComponent. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ElectricCurrentPDEComponent.html 年