ElectricPotentialCondition[pred,vars,pars]
represents an electric potential surface boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
ElectricPotentialCondition[pred,vars,pars,lkey]
represents an electric potential surface boundary condition with local parameters specified in pars[lkey].


ElectricPotentialCondition
ElectricPotentialCondition[pred,vars,pars]
represents an electric potential surface boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
ElectricPotentialCondition[pred,vars,pars,lkey]
represents an electric potential surface boundary condition with local parameters specified in pars[lkey].
Details


- ElectricPotentialCondition specifies a Dirichlet boundary condition for ElectrostaticPDEComponent and ElectricCurrentPDEComponent.
- ElectricPotentialCondition specifies a boundary condition for ElectrostaticPDEComponent and ElectricCurrentPDEComponent.
- ElectricPotentialCondition is typically used to set a specific electric potential on the boundary. Common examples include capacitive devices charged by applying a voltage difference.
- ElectricPotentialCondition sets a specific electric potential on the boundary with dependent variable
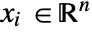 and independent variables
and independent variables 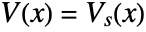 .
. - Stationary variables vars are vars={V[x1,…,xn],{x1,…,xn}}.
- Frequency-dependent variables vars are vars={V[x1,…,xn],ω,{x1,…,xn}}.
- The stationary or frequency domain electric potential condition ElectricPotentialCondition model
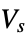 where
where 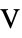 [
[![TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF]](Files/ElectricPotentialCondition.en/6.png) ] is a given surface potential.
] is a given surface potential. - The following additional model parameters pars can be given:
-
parameter default symbol "ElectricPotential" - 0
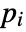 , surface electric potential in [
, surface electric potential in [![TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF]](Files/ElectricPotentialCondition.en/8.png) ]
] - Model parameters pars are specified as for ElectrostaticPDEComponent and ElectricCurrentPDEComponent.
- A prescribed electric potential condition boundary can be used with:
-
analysis type applicable Frequency Response Yes Stationary Yes - ElectricPotentialCondition evaluates to a DirichletCondition.
- The boundary predicate pred can be specified as in DirichletCondition.
- If the ElectricPotentialCondition depends on parameters
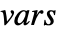 that are specified in the association pars as …,keypi…,pivi,…, the parameters
that are specified in the association pars as …,keypi…,pivi,…, the parameters 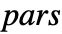 are replaced with
are replaced with 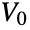 .
.
Examples
open all close allBasic Examples (3)
Set up an electric potential surface boundary condition:
Set up a default electric potential surface boundary condition:
Compute the electric potential distribution with model variables ![]() and parameters
and parameters ![]() with an electric potential
with an electric potential ![]() of
of ![]() [
[![]() ] at the left boundary and a ground potential at the right boundary.
] at the left boundary and a ground potential at the right boundary.
Specify model variables and electrostatic parameters:
Scope (4)
Define model variables vars for an electrostatic analysis with model parameters pars and multiple specific parameter boundary conditions:
1D (1)
Compute the electric potential distribution between two parallel plates separated by a distance ![]() [
[![]() ] and positioned normal to the
] and positioned normal to the ![]() axis. The left plate is maintained at a constant potential
axis. The left plate is maintained at a constant potential ![]() [
[![]() ], whereas the right plate is grounded,
], whereas the right plate is grounded, ![]() . The region between the plates is characterized by a relative permittivity
. The region between the plates is characterized by a relative permittivity ![]() and a uniform electron charge density
and a uniform electron charge density ![]() [
[![]() ]. The equation to use in the model is given by:
]. The equation to use in the model is given by:
Set up the electrostatic model variables ![]() :
:
Specify electrostatic model parameters:
2D (1)
Solve for the electric scalar potential in a three-bar electric switch with an electrical conductivity of ![]() . The equation to use in the model is given by:
. The equation to use in the model is given by:
Set up the electrostatic model variables ![]() :
:
Specify an electrical conductivity ![]() :
:
Specify ground potential at the lower boundary:
Specify an electric potential of ![]() [
[![]() ] at the upper boundary:
] at the upper boundary:
3D (1)
Model a simplified bushing insulator of a transformer with an electric potential condition at the inner walls, which are in contact with the high-voltage conductor, and a ground potential boundary at one of the surface plates (![]() ). The equation to use in the model is given by:
). The equation to use in the model is given by:
Set up the electrostatic model variables ![]() :
:
Specify a relative permittivity ![]() :
:
Specify a ground potential at the surface ![]() :
:
Tech Notes
Related Guides
Text
Wolfram Research (2024), ElectricPotentialCondition, Wolfram Language function, https://reference.wolfram.com/language/ref/ElectricPotentialCondition.html (updated 2024).
CMS
Wolfram Language. 2024. "ElectricPotentialCondition." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/ElectricPotentialCondition.html.
APA
Wolfram Language. (2024). ElectricPotentialCondition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ElectricPotentialCondition.html
BibTeX
@misc{reference.wolfram_2025_electricpotentialcondition, author="Wolfram Research", title="{ElectricPotentialCondition}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/ElectricPotentialCondition.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_electricpotentialcondition, organization={Wolfram Research}, title={ElectricPotentialCondition}, year={2024}, url={https://reference.wolfram.com/language/ref/ElectricPotentialCondition.html}, note=[Accessed: 10-March-2026]}