ElectrostaticPDEComponent

ElectrostaticPDEComponent[vars,pars]

yields an electrostatic PDE term with variables vars and parameters pars.

Details

  • ElectrostaticPDEComponent is typically used to generate an electrostatic equation with model variables vars and model parameters pars.
  • ElectrostaticPDEComponent returns a sum of differential operators to be used as a part of partial differential equations:
  • ElectrostaticPDEComponent models static electric fields produced by stationary charges in insulating, or dielectric materials.
  • ElectrostaticPDEComponent models electrostatic phenomena with the dependent variable 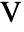, the electric scalar potential. 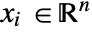is in units of volt [TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF]], independent variables 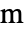in units of [TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]].
  • Stationary variables vars are vars={V[x1,…,xn],{x1,…,xn}}.
  • ElectrostaticPDEComponent generally does not produces a time-dependent PDE.
  • ElectrostaticPDEComponent is based on a diffusion, a source and a derivative PDE term:
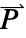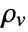  • is the vacuum permittivity in units of [TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF]], the polarization vector in units of [TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]] and 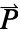the volume charge density in units of [TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 3}}, coulombs per meter cubed, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]].
  • The polarization vector 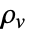specifies the density of permanent or induced electric dipole moments inside a material.
  • The volume charge density 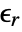models charge distributions, negative or positive.
  • ElectrostaticPDEComponent can produce different equations, depending on the constitutive relationship.
  • For linear materials, the ElectrostaticPDEComponent equation simplifies to:
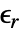  • is the unitless relative permittivity.
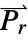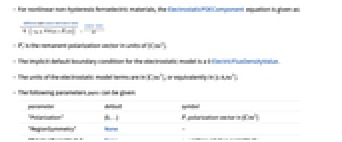
  • can be isotropic, orthotropic or anisotropic.
  • For nonlinear non-hysteresis ferroelectric materials, the ElectrostaticPDEComponent equation is given as:
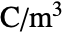  • is the remanent polarization vector in units of [TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]].
  • The implicit default boundary condition for the electrostatic model is a 0 ElectricFluxDensityValue.
  • The units of the electrostatic model terms are in [TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 3}}, coulombs per meter cubed, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]], or equivalently in [TemplateBox[{InterpretationBox[, 1], {"s", , "A", , "/", , {"m", ^, 3}}, second amperes per meter cubed, {{(, {"Amperes", , "Seconds"}, )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]].
  • The following parameters pars can be given:
  • parameterdefaultsymbol
    "Polarization"{0,…}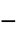, polarization vector in [TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]]
    "RegionSymmetry"None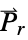
    "RelativePermittivity"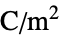
  • , unitless relative permittivity
    • "RemanentPolarization"{0,…}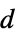, remanent polarization vector in [TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]]
    "Thickness"1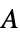, thickness in [TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]]
    "CrossSectionalArea"1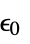, cross-sectional area in [TemplateBox[{InterpretationBox[, 1], {{"m", ^, 2}}, meters squared, {"Meters", ^, 2}}, QuantityTF]]
    		"VacuumPermittivity"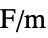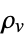, vacuum permittivity in [TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF]]
    "VolumeChargeDensity"0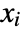, volume charge density in [TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 3}}, coulombs per meter cubed, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]]
  • All parameters may depend on the spacial variable 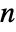and dependent variable .
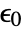  • The number of independent variables 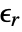determines the dimensions of 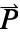or 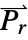and the length of vectors and .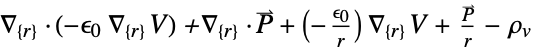
  • A possible choice for the parameter "RegionSymmetry" is "Axisymmetric".
  • "Axisymmetric" region symmetry represents a truncated cylindrical coordinate system where the cylindrical coordinates are reduced by removing the angle variable as follows:
  • dimensionreductionequation
    1D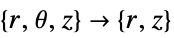
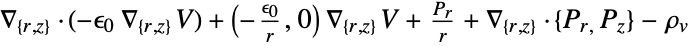
    2D
  • In 2D, when a "Thickness" 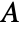is specified, the ElectrostaticPDEComponent equation is given as:
  • In 1D, when a "CrossSectionalArea" 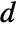is specified, the ElectrostaticPDEComponent equation is given as:
  • In a 1D axisymmetric, when a "Thickness" 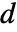is specified, the ElectrostaticPDEComponent equation is given as:
  • The input specification for the parameters is exactly the same as for their corresponding operator terms.
  • If no parameters are specified, the default electrostatic PDE is:
  • If the ElectrostaticPDEComponent depends on parameters 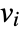that are specified in the association pars as …,keypi…,pivi,…], the parameters 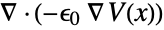are replaced with .

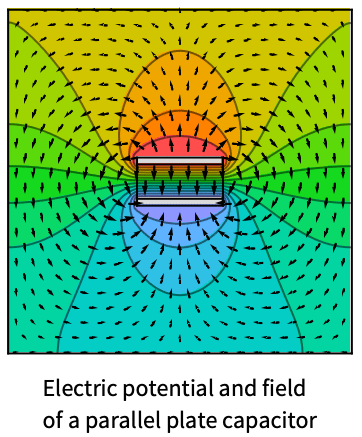
Examples

open allclose all

Basic Examples  (3)

Define an electrostatic model :

Set up an electrostatic model with particular material parameters:

Specify model variables and electrostatic parameters:

Set up and solve an electrostatic PDE:

Visualize the solution:

Scope  (14)

1D  (4)

Define a 1D electrostatic model with a cross-sectional area :

Model an electric potential field with two electric potential conditions at the sides.

Specify model variables and electrostatic parameters:

Set up and solve an electrostatic PDE:

Visualize the solution:

Model an electric potential field with two electric potential conditions at the sides and a discontinuous relative permittivity.

Specify model variables and electrostatic parameters:

Set up and solve an electrostatic PDE:

Visualize the solution:

2D  (5)

Define a 2D electrostatic model with a polarization vector:

Define a 2D nonlinear electrostatic model with a remanent polarization vector:

Define a 2D electrostatic model with a thickness :

Define an orthotropic relative permittivity:

Define a fully anisotropic relative permittivity:

2D Axisymmetric  (2)

Define a 2D axisymmetric electrostatic model:

Define a 2D axisymmetric orthotropic electrostatic model:

3D  (1)

Model an electric potential field in a hollow ball with electric potential conditions at the inner and outer radii.

Specify model variables and electrostatic parameters:

Set up and solve an electrostatic PDE:

Visualize the solution:

Multi-material  (2)

Set up an electrostatic model for several material regions:

Model an electric potential field with two electric potential conditions at the sides and a discontinuous relative permittivity.

Specify model variables and electrostatic parameters:

Set up and solve an electrostatic PDE:

Visualize the solution:

Applications  (4)

1D  (2)

Compute the electric potential distribution between two parallel plates separated by a distance [TemplateBox[{InterpretationBox[, 1], "cm", centimeters, "Centimeters"}, QuantityTF]] and positioned normal to the axis. The left plate is maintained at a constant potential [TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF]], whereas the right plate is grounded, [TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF]]. The region between the plates is characterized by a relative permittivity and a uniform electron charge density [TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 3}}, coulombs per meter cubed, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]]. The equation to model is given by:

del .(-epsilon_0epsilon_r del V(x))^(︷^( electrostatic model)) =rho_v

Set up the electrostatic model variables vars:

Set up a region :

Specify electrostatic model parameters:

Specify the electric potential conditions:

Set up the equation:

Solve the PDE:

Visualize the solution:

Compute the electrical potential distribution between two parallel plates with the same distance and boundary conditions as in the previous example, but now with a nonuniform charge distribution given by:

Set up the electrostatic model variables vars:

Set up a region :

Specify electrostatic model parameters:

Specify the electric potential conditions:

Set up the equation:

Solve the PDE:

Visualize the solution:

2D  (1)

Model an infinitely long rectangular box with metallic walls. The box has a width of [TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]], and a height of [TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]]. The side and bottom walls are maintained at zero electric potential, whereas the top wall has a fixed electric potential of . The region inside the box is free of charge . The equation to model is given by:

del .(-epsilon_0epsilon_r del V(x,y))^(︷^( electrostatic model)) =0

Define the model variables and parameters:

Set up the model region:

Set up a 2D electrostatic model:

The side and bottom walls at , and are maintained at a zero electric potential:

The top wall at is fixed with an electric potential of [TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF]]:

Set up the equation:

Solve the PDE:

Visualize the solution:

3D  (1)

Model a dielectric material of a cylindrical capacitor with two electric potential conditions at the upper and lower boundaries, which represent the capacitor electrodes. The equation to model is given by:

del .(-epsilon_0epsilon_r del V(x,y,z))^(︷^( electrostatic model)) =0

Set up the electrostatic model variables vars:

Set up a region :

Specify a relative permittivity :

Specify ground potential at the lower boundary:

Specify an electric potential of [TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF]] at the upper boundary:

Set up the equation:

Solve the PDE:

Visualize the solution:

Possible Issues  (1)

For symbolic computation, the "VacuumPermittivity" or "RelativePermittivity" parameter should be given as a matrix:

For numeric values, the "VacuumPermittivity" or "RelativePermittivity" parameter is automatically converted to a matrix of proper dimensions:

This automatic conversion is not possible for symbolic input:

Not providing the properly dimensioned matrix will result in an error:

Wolfram Research (2024), ElectrostaticPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/ElectrostaticPDEComponent.html (updated 2024).

Text

Wolfram Research (2024), ElectrostaticPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/ElectrostaticPDEComponent.html (updated 2024).

CMS

Wolfram Language. 2024. "ElectrostaticPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/ElectrostaticPDEComponent.html.

APA

Wolfram Language. (2024). ElectrostaticPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ElectrostaticPDEComponent.html

BibTeX

@misc{reference.wolfram_2024_electrostaticpdecomponent, author="Wolfram Research", title="{ElectrostaticPDEComponent}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/ElectrostaticPDEComponent.html}", note=[Accessed: 04-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_electrostaticpdecomponent, organization={Wolfram Research}, title={ElectrostaticPDEComponent}, year={2024}, url={https://reference.wolfram.com/language/ref/ElectrostaticPDEComponent.html}, note=[Accessed: 04-November-2024 ]}