EllipticPi[n,m]
第3種完全楕円積分 ![]() を与える.
を与える.
EllipticPi[n,ϕ,m]
不完全楕円積分 ![]() を与える.
を与える.




EllipticPi
EllipticPi[n,m]
第3種完全楕円積分 ![]() を与える.
を与える.
EllipticPi[n,ϕ,m]
不完全楕円積分 ![]() を与える.
を与える.
詳細

- 記号操作・数値操作の両方に適した数学関数である.
- 実数
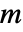 および
および 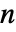 について,
について,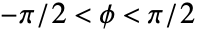 ,
,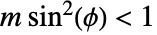 のとき
のとき![TemplateBox[{n, phi, m}, EllipticPi3]=int_0^phi(1-n sin^2(theta))^(-1)[1-m sin^2(theta)]^(-1/2)dtheta TemplateBox[{n, phi, m}, EllipticPi3]=int_0^phi(1-n sin^2(theta))^(-1)[1-m sin^2(theta)]^(-1/2)dtheta](Files/EllipticPi.ja/7.png) .ただし,主値積分は
.ただし,主値積分は 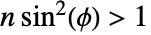 について既知である.
について既知である. -
![TemplateBox[{n, m}, EllipticPi]=TemplateBox[{n, {pi, /, 2}, m}, EllipticPi3] TemplateBox[{n, m}, EllipticPi]=TemplateBox[{n, {pi, /, 2}, m}, EllipticPi3]](Files/EllipticPi.ja/9.png)
- EllipticPi[n,m]は,
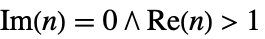 および
および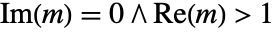 に不連続な分枝切断線を持つ.
に不連続な分枝切断線を持つ. - EllipticPi[n,ϕ,m]は,
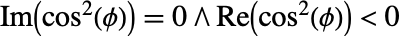 ,
,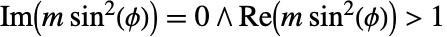 ,
,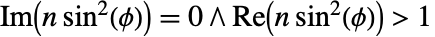 に不連続な分枝切断線を持つ.
に不連続な分枝切断線を持つ. - 特別な引数の場合,EllipticPiは,自動的に厳密値を計算する.
- EllipticPiは任意の数値精度で評価できる.
- EllipticPi自動的にリストに縫い込まれる.
- EllipticPiはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
例題
すべて開く すべて閉じる例 (6)
Infinityにおける級数展開:
スコープ (36)
数値評価 (6)
EllipticPiを高精度で効率よく評価する:
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する:
Aroundを使って平均的な場合の統計区間を計算することもできる:
MatrixFunctionを使って行列のEllipticPi関数を計算することもできる:
可視化 (4)
EllipticPiを,第2パラメータ ![]() のさまざまな値についてプロットする:
のさまざまな値についてプロットする:
EllipticPiを,第1パラメータ ![]() のさまざまな値についてプロットする:
のさまざまな値についてプロットする:
関数の特性 (9)
EllipticPiは解析関数ではない:
EllipticPiは有理型関数ではない:
級数展開 (3)
関数表現 (4)
アプリケーション (6)
点![]() から
から ![]() ,
, ![]() 平面上の原点の円板(例えば探知機や道路標識等)によって範囲を定められた立体角の定義:
平面上の原点の円板(例えば探知機や道路標識等)によって範囲を定められた立体角の定義:
この動作は EllipticPiを使って表すことができる(簡潔を期するため,出現する根は省略されている):
種数1の定数平均曲率ウェンテ(Wente)トーラスのパラメーター化:
EllipticPiについてのパラメータのさまざまな変化を数値的に確認する:
特性と関係 (4)
関連項目
EllipticK EllipticF EllipticE CarlsonRM CarlsonRJ CarlsonRC
Function Repository: BulirschCEL BulirschEL3 BulirschEL HeumanLambda
テクニカルノート
履歴
1988 で導入 (1.0) | 2020 で更新 (12.2) ▪ 2021 (13.0) ▪ 2022 (13.1)
テキスト
Wolfram Research (1988), EllipticPi, Wolfram言語関数, https://reference.wolfram.com/language/ref/EllipticPi.html (2022年に更新).
CMS
Wolfram Language. 1988. "EllipticPi." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/EllipticPi.html.
APA
Wolfram Language. (1988). EllipticPi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EllipticPi.html
BibTeX
@misc{reference.wolfram_2025_ellipticpi, author="Wolfram Research", title="{EllipticPi}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/EllipticPi.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_ellipticpi, organization={Wolfram Research}, title={EllipticPi}, year={2022}, url={https://reference.wolfram.com/language/ref/EllipticPi.html}, note=[Accessed: 05-February-2026]}