EllipticK

EllipticK[m]

gives the complete elliptic integral of the first kind TemplateBox[{m}, EllipticK].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • EllipticK is given in terms of the incomplete elliptic integral of the first kind by TemplateBox[{m}, EllipticK]=TemplateBox[{{pi, /, 2}, m}, EllipticF].
  • EllipticK[m] has a branch cut discontinuity in the complex m plane running from 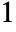to .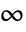
  • For certain special arguments, EllipticK automatically evaluates to exact values.
  • EllipticK can be evaluated to arbitrary numerical precision.
  • EllipticK automatically threads over lists.
  • EllipticK can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (5)

Evaluate numerically:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Series expansion at the origin:

Series expansion at Infinity:

Scope  (38)

Numerical Evaluation  (5)

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Evaluate numerically for complex arguments:

Evaluate EllipticK efficiently at high precision:

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

Or compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix EllipticK function using MatrixFunction:

Specific Values  (5)

Simple exact values are generated automatically:

Some exact values in terms of Gamma after applying FunctionExpand:

Find directional limiting values at branch cuts:

Value at infinity:

Find the root of the equation TemplateBox[{m}, EllipticK]=2:

Visualization  (2)

Plot EllipticK:

Plot the real part of TemplateBox[{z}, EllipticK]:

Plot the imaginary part of TemplateBox[{z}, EllipticK]:

Function Properties  (9)

EllipticK is defined for all real values less than 1:

EllipticK takes all real positive values:

EllipticK is not an analytic function:

Has both singularities and discontinuities:

EllipticK is not a meromorphic function:

EllipticK is nondecreasing on its domain:

EllipticK is injective:

EllipticK is not surjective:

EllipticK is non-negative on its domain:

EllipticK is convex on its domain:

Differentiation  (3)

First derivative:

Higher derivatives:

Formula for the ^(th) derivative:

Integration  (3)

Indefinite integral of EllipticK:

Definite integral over an interval lying on the branch cut:

More integrals:

Series Expansions  (3)

Taylor expansion for EllipticK:

Plot the first three approximations for EllipticK around :

Series expansions at branch points:

EllipticK can be applied to power series:

Integral Transforms  (3)

Compute the Laplace transform using LaplaceTransform:

MellinTransform:

HankelTransform:

Function Representations  (5)

Relation to other elliptic integrals:

Relation to the LegendreP:

Represent in terms of MeijerG using MeijerGReduce:

EllipticK can be represented as a DifferentialRoot:

TraditionalForm formatting:

Applications  (7)

Small-angle approximation to the period of a pendulum:

Plot the period versus the initial angle:

Vector potential due to a circular current flow, in cylindrical coordinates:

The components of the magnetic field:

Plot the magnitude of the magnetic field:

Resistance between the origin and the point in an infinite 3D lattice of unit resistors:

Energy for the Onsager solution of the Ising model:

Plot of the specific heat:

Find the critical temperature:

Calculate a singular value:

Current flow in a rectangular conducting sheet with voltage applied at a pair of opposite corners:

Plot the flow lines with bounds defined via EllipticK:

Construct lowpass elliptic filter for analog signal:

Compute filter ripple parameters and associate elliptic function parameter:

Use elliptic degree equation to find the ratio of the pass and the stop frequencies:

Compute corresponding stop frequency and elliptic parameters:

Compute ripple locations and poles and zeros of the transfer function:

Compute poles of the transfer function:

Assemble the transfer function:

Compare with the result of EllipticFilterModel:

Properties & Relations  (4)

This shows the branch cuts of the EllipticK function:

Numerically find a root of a transcendental equation:

Solve a differential equation:

EllipticK is a particular case of various mathematical functions:

Possible Issues  (3)

Machine-precision evaluation can result in numerically inaccurate answers near branch cuts:

The defining integral converges only under additional conditions:

Different argument conventions exist that result in modified results:

Neat Examples  (2)

Probability that a random walker in a 3D cubic lattice returns to the origin:

Carry out a modeling run of 1000 walks and count how many it returns to the origin:

Compare with the expected count at :

Riemann surface of TemplateBox[{m}, EllipticK]:

Wolfram Research (1988), EllipticK, Wolfram Language function, https://reference.wolfram.com/language/ref/EllipticK.html (updated 2022).

Text

Wolfram Research (1988), EllipticK, Wolfram Language function, https://reference.wolfram.com/language/ref/EllipticK.html (updated 2022).

CMS

Wolfram Language. 1988. "EllipticK." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/EllipticK.html.

APA

Wolfram Language. (1988). EllipticK. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EllipticK.html

BibTeX

@misc{reference.wolfram_2024_elliptick, author="Wolfram Research", title="{EllipticK}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/EllipticK.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_elliptick, organization={Wolfram Research}, title={EllipticK}, year={2022}, url={https://reference.wolfram.com/language/ref/EllipticK.html}, note=[Accessed: 22-December-2024 ]}