EulerAngles

EulerAngles[r]

gives Euler angles {α,β,γ} corresponding to the rotation matrix r.

EulerAngles[r,{a,b,c}]

gives Euler angles {α,β,γ} with rotation order {a,b,c}.

Details

  • EulerAngles[r,{a,b,c}] gives angles {α,β,γ} such that EulerMatrix[{α,β,γ},{a,b,c}]r.
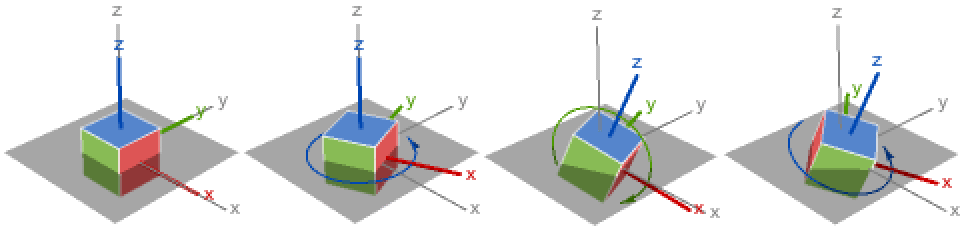
  • EulerAngles[r] is equivalent to EulerAngles[r,{3,2,3}], the z-y-z rotations.
  • The default z-y-z angles EulerAngles[r,{3,2,3}] decomposes rotation into three steps:
  • The rotation axes a, b, and c can be any integer 1, 2, or 3. But there are only twelve combinations that are general enough to be able to specify any 3D rotation.
  • Rotations with the first and last axis repeated:
  • {3,2,3}z-y-z rotation (default)
    {3,1,3}z-x-z rotation
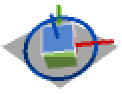
    {2,3,2}y-z-y rotation
    {2,1,2}y-x-y rotation
    {1,3,1}x-z-x rotation
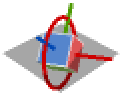
    {1,2,1}x-y-x rotation
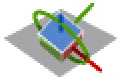
  • Rotations with all three axes different:
  • {1,2,3}x-y-z rotation
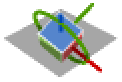
    {1,3,2}x-z-y rotation
    {2,1,3}y-x-z rotation
    {2,3,1}y-z-x rotation
    {3,1,2}z-x-y rotation
    {3,2,1}z-y-x rotation
  • Rotations with subsequent axes repeated may not be invertible, since these are not capable of representing all possible rotations in 3D.

Examples

open allclose all

Basic Examples  (2)

Get Euler angles from the rotation matrix:

Get Euler angles from the rotation matrix with the given rotation order:

Applications  (6)

Rotation Representations  (4)

Convert Euler angles from one rotation order to another:

Convert roll-pitch-yaw angles to Euler angles:

Get Euler angles for a 3D rotation in the plane given by t{1,1,1} + s{1,–2,1}:

Find a single set of Euler angles from a composition of Euler rotations:

Both perform the same transformation (red):

Coordinate Systems  (2)

Let and be the coordinate axes for two orthogonal coordinate systems that are rotated from each other:

Given TemplateBox[{{{, {{x, _, 2}, ,, {y, _, 2}, ,, {z, _, 2}}, }}}, Transpose]=R.TemplateBox[{{{, {{x, _, 1}, ,, {y, _, 1}, ,, {z, _, 1}}, }}}, Transpose], where the rotated axis is given by etc., one then finds that R=TemplateBox[{{{, {{x, _, 2}, ,, {y, _, 2}, ,, {z, _, 2}}, }}}, Transpose].{x_1,y_1,z_1}, since TemplateBox[{{{, {{x, _, 1}, ,, {y, _, 1}, ,, {z, _, 1}}, }}}, Transpose] is an orthogonal matrix and its inverse is its transpose:

Verify that is the rotation that relates the coordinate systems:

Find the corresponding Euler angles that define :

Visualize:

The right-handed, z-up coordinate system is standard for Cartesian coordinates in mathematics. However, in computer graphics applications, different systems, such as right-handed, y-up may be used. Using the previous example, find the Euler angles that transform a z-up to a y-up coordinate system:

Obtain the rotation matrix and the corresponding Euler angles that define :

Use those angles to transform the y-up coordinate system and visualize (z-up system, y-up system, and transformed y-up system):

Properties & Relations  (1)

EulerAngles returns angles for which EulerMatrix gives the same rotation matrix:

The angles need not be the same:

However, both sets of angles produce the same rotation matrix:

Possible Issues  (1)

EulerMatrix allows equal consecutive axes and this generates a rotation matrix:

However, EulerAngles requires consecutive axes to be distinct:

This is because with consecutive axes equal, some rotation matrices cannot be represented:

Wolfram Research (2015), EulerAngles, Wolfram Language function, https://reference.wolfram.com/language/ref/EulerAngles.html.

Text

Wolfram Research (2015), EulerAngles, Wolfram Language function, https://reference.wolfram.com/language/ref/EulerAngles.html.

CMS

Wolfram Language. 2015. "EulerAngles." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/EulerAngles.html.

APA

Wolfram Language. (2015). EulerAngles. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EulerAngles.html

BibTeX

@misc{reference.wolfram_2025_eulerangles, author="Wolfram Research", title="{EulerAngles}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/EulerAngles.html}", note=[Accessed: 03-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_eulerangles, organization={Wolfram Research}, title={EulerAngles}, year={2015}, url={https://reference.wolfram.com/language/ref/EulerAngles.html}, note=[Accessed: 03-July-2025 ]}