EulerMatrix

EulerMatrix[{α,β,γ}]

gives the Euler 3D rotation matrix formed by rotating by α around the current axis, then by β around the current axis, and then by γ around the current axis.

EulerMatrix[{α,β,γ},{a,b,c}]

gives the Euler 3D rotation matrix corresponding, first rotating by α around the current a axis, then by β around the current b axis, and finally by γ around the current c axis.

Details and Options

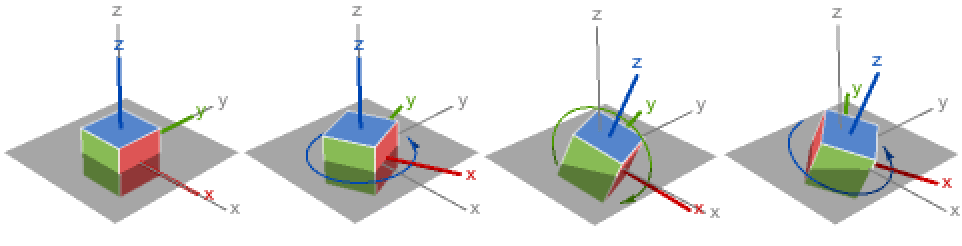
  • EulerMatrix is also known as Euler rotation matrix or Euler rotation, and the angles α, β, and γ are often referred to as Euler angles.
  • EulerMatrix is typically used to specify a rotation as a sequence of basic rotations around coordinate axes where each subsequent rotation is referring to the current or intrinsic coordinate frame.
  • EulerMatrix[{α,β,γ}] is equivalent to EulerMatrix[{α,β,γ},{3,2,3}].
  • The default z-y-z rotation EulerMatrix[{α,β,γ},{3,2,3}]:
  • EulerMatrix[{α,β,γ},{a,b,c}] is equivalent to 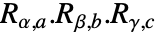, where Rα,a=RotationMatrix[α,UnitVector[3,a]] etc. »
  • The x-y-z rotation EulerMatrix[{α,β,γ},{1,2,3}]:
  • The rotation axes a, b, and c can be any integer 1, 2, or 3, but there are only 12 combinations that are general enough to be able to specify any 3D rotation.
  • Rotations with the first and last axis repeated:
  • {3,2,3}z-y-z rotation (default)
    {3,1,3}z-x-z rotation
    {2,3,2}y-z-y rotation
    {2,1,2}y-x-y rotation
    {1,3,1}x-z-x rotation
    {1,2,1}x-y-x rotation
  • Rotations with all three axes different:
  • {1,2,3}x-y-z rotation
    {1,3,2}x-z-y rotation
    {2,1,3}y-x-z rotation
    {2,3,1}y-z-x rotation
    {3,1,2}z-x-y rotation
    {3,2,1}z-y-x rotation
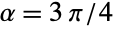
  • Rotations with subsequent axes repeated still produce a rotation matrix but cannot be inverted uniquely using EulerAngles.
  • EulerMatrix supports the option TargetStructure, which specifies the structure of the returned matrix. Possible settings for TargetStructure include:
  • Automaticautomatically choose the representation returned
    "Dense"represent the matrix as a dense matrix
    "Orthogonal"represent the matrix as an orthogonal matrix
    "Unitary"represent the matrix as a unitary matrix
  • EulerMatrix[…,TargetStructureAutomatic] is equivalent to EulerMatrix[…,TargetStructure"Dense"].

Examples

open allclose all

Basic Examples  (2)

The standard Euler matrix:

Rotate an axes-aligned unit cube:

Scope  (6)

Give the standard z-y-z Euler rotation matrix with , , and :

Rotate the vector {1,0,0}:

Visualize the rotated vector (red):

Give an x-y-x Euler rotation matrix by specifying the second argument:

Rotate and visualize the vector {1,0,0}:

Give an x-y-z Euler rotation matrix:

Rotate and visualize the vector {1,0,0}:

Rotate primitives in 3D graphics using GeometricTransformation:

Rotate a region using TransformedRegion:

Rotate a 3D image using ImageTransformation:

Options  (1)

TargetStructure  (1)

Return the Euler rotation matrix as a dense matrix:

Return the Euler rotation matrix as an orthogonal matrix:

Return the Euler rotation matrix as a unitary matrix:

Applications  (6)

Illustrations  (1)

Build a function that illustrates Euler rotations, showing the axis that is being rotated around:

Here are all six of the a-b-a axes rotations. First is the standard z-y-z Euler rotation:

The x-y-x Euler rotation:

The x-z-x Euler rotation:

The y-x-y Euler rotation:

The y-z-y Euler rotation:

The z-x-z Euler rotation:

Then there are the six a-b-c axes rotations. First is the x-y-z Euler rotation:

The x-z-y Euler rotation:

The y-x-z Euler rotation:

The y-z-x Euler rotation:

The z-x-y Euler rotation:

The z-y-x Euler rotation:

Gimbals  (5)

A gimbal is a system of pivoted rings that allows an object to orient itself in an arbitrary direction. These are used in various navigation and imaging applications:

The orientation of the object within a gimbal can be modeled using EulerMatrix with the angles of the rings' rotations, from the outermost to the innermost rings. Note that an a-b-a axis system is used:

A gimbal with a-b-c axis rotations models a gimbal system with an initial state where all rings' axes are perpendicular to each other:

This uses the z-y-x Euler rotation:

A rotation system may enter gimbal lock, a situation where a certain angle value reduces the system's degrees of freedom. The normal, non-locked case produces the following:

The vector {1,1,0} can be rotated to an arbitrary point on a surface:

In the locked case, only the difference can affect the rotation:

Now the vector {1,1,0} can only be rotated to a point on a curve:

When axes , gimbal lock will occur when . Here is an example x-y-x rotation:

The non-locked m1 and locked m2 cases:

Unlocked m1 and locked m2 cases for z-y-z rotation:

And when axes are all different , gimbal lock will occur when . Here is an example x-y-z rotation:

The locked m1 and unlocked m2 cases:

Locked m1 and unlocked m2 cases for y-x-z rotation:

Properties & Relations  (11)

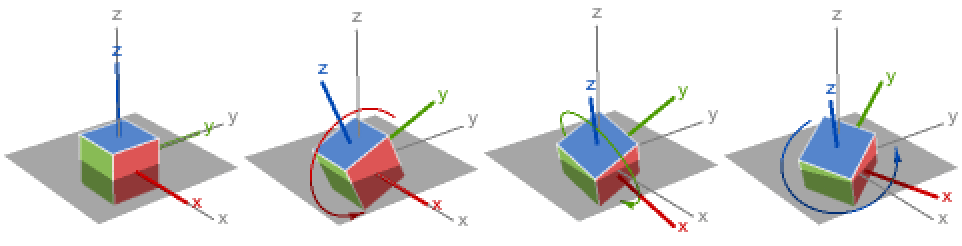
EulerMatrix corresponds to three rotations:

With general ordering of rotation axes:

Use EulerAngles to return angles that produce the same rotation matrix:

The angles need not be the same:

However, both sets of angles produce the same rotation matrix:

Use RollPitchYawMatrix for rotations wrt the global coordinate frame in each step:

EulerMatrix rotates wrt the current coordinate frame in each step:

If two subsequent rotation axes are identical, i.e. or , the system has two degrees of freedom, such as when performing an x-y-y rotation:

If all rotation axes are identical, i.e. , the system has only one degree of freedom, such as when performing an x-x-x rotation:

EulerMatrix[{α,β,γ},{a,b,c}] is the same as RollPitchYawMatrix[{γ,β,α},{c,b,a}]:

EulerMatrix only applies in :

For general dimension, use RotationMatrix:

EulerMatrix parametrizes any rotation in terms of three axis-oriented rotations:

For rotations around a general axis, use RotationMatrix:

EulerMatrix is an orthogonal matrix with determinant 1:

The inverse of an EulerMatrix is its transpose:

The inverse of EulerMatrix[{α,β,γ}] is EulerMatrix[{-γ,-β,-α}]:

The inverse of EulerMatrix[{α,β,γ},{a,b,c}] is EulerMatrix[{-γ,-β,-α},{c,b,a}]:

Possible Issues  (1)

EulerMatrix allows equal consecutive axes, and this generates a rotation matrix:

However, EulerAngles requires consecutive axes to be distinct:

This is because with consecutive axes equal, some rotation matrices cannot be represented:

Neat Examples  (1)

Use GeometricTransformation to visualize the rotation of a sphere by a range of angles:

Wolfram Research (2015), EulerMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/EulerMatrix.html (updated 2024).

Text

Wolfram Research (2015), EulerMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/EulerMatrix.html (updated 2024).

CMS

Wolfram Language. 2015. "EulerMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/EulerMatrix.html.

APA

Wolfram Language. (2015). EulerMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EulerMatrix.html

BibTeX

@misc{reference.wolfram_2024_eulermatrix, author="Wolfram Research", title="{EulerMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/EulerMatrix.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_eulermatrix, organization={Wolfram Research}, title={EulerMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/EulerMatrix.html}, note=[Accessed: 21-November-2024 ]}