EulerMatrix

EulerMatrix[{α,β,γ}]

给出欧拉三维旋转矩阵，通过绕当前 轴旋转 α，再绕当前 轴旋转 β，然后再绕当前 轴旋转 γ 得到.

EulerMatrix[{α,β,γ},{a,b,c}]

给出欧拉三维旋转矩阵，相应于首先绕当前 a 轴旋转 α，再绕当前 b 轴旋转 β，最后绕当前 c 轴旋转 γ.

更多信息和选项

  • EulerMatrix 也称为欧拉旋转矩阵或者欧拉旋转，角度 α、β 和 γ 通常称为欧拉角.
  • EulerMatrix 通常用于将旋转指定为沿着坐标轴的基本旋转序列，其中每个相连的旋转称为当前或者固有的坐标框架.
  • EulerMatrix[{α,β,γ}] 等价于 EulerMatrix[{α,β,γ},{3,2,3}].
  • 默认 z-y-z 旋转 EulerMatrix[{α,β,γ},{3,2,3}]：
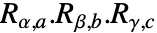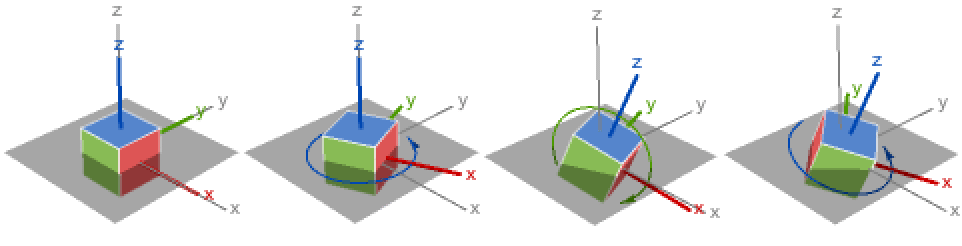
  • EulerMatrix[{α,β,γ},{a,b,c}] 等价于 ，其中 Rα,a=RotationMatrix[α,UnitVector[3,a]] 等. »
  • x-y-z 旋转 EulerMatrix[{α,β,γ},{1,2,3}]：
  • 旋转轴 a、b 和 c 可以是任何整数1、2或者3，但是只有12个足够普适的组合可以指定任意三维旋转.
  • 第一个和最后一个轴相同的旋转：
  • {3,2,3}z-y-z 旋转（默认
    {3,1,3}z-x-z 旋转
    {2,3,2}y-z-y 旋转
    {2,1,2}y-x-y 旋转
    {1,3,1}x-z-x 旋转
    {1,2,1}x-y-x 旋转
  • 具有三个完全不同的轴的旋转：
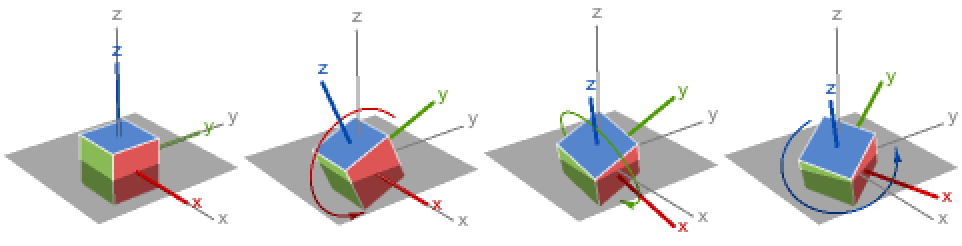
  • {1,2,3}x-y-z 旋转
    {1,3,2}x-z-y 旋转
    {2,1,3}y-x-z 旋转
    {2,3,1}y-z-x 旋转
    {3,1,2}z-x-y 旋转
    {3,2,1}z-y-x 旋转
  • 相邻轴重复的旋转仍然能生成旋转矩阵，但是无法使用 EulerAngles.
  • EulerMatrix 支持 TargetStructure 选项，该选项指定了返回矩阵的结构. TargetStructure 的可能设置包括：
  • Automatic自动选择返回的表示
    "Dense"将矩阵表示为密集矩阵
    "Orthogonal"将矩阵表示为正交矩阵
    "Unitary"将矩阵表示为酉矩阵
  • EulerMatrix[…,TargetStructureAutomatic] 等价于 EulerMatrix[…,TargetStructure"Dense"].

范例

打开所有单元关闭所有单元

基本范例  (2)

标准欧拉矩阵：

旋转轴对齐的单位立方体：

范围  (6)

在 、 和 下，给出标准 z-y-z 欧拉旋转矩阵：

旋转向量{1,0,0}：

可视化旋转向量（红色）：

通过指定第二个参数，给出 x-y-x 欧拉旋转矩阵：

旋转并且可视化向量 {1,0,0}:

给出 x-y-z 欧拉旋转矩阵：

旋转并且可视化向量 {1,0,0}：

使用 GeometricTransformation 旋转三维图形中的基元：

使用 TransformedRegion 旋转区域：

使用 ImageTransformation 旋转三维图像：

选项  (1)

TargetStructure  (1)

Return the Euler rotation matrix as a dense matrix:

Return the Euler rotation matrix as an orthogonal matrix:

Return the Euler rotation matrix as a unitary matrix:

应用  (6)

显示  (1)

构建一个显示欧拉旋转的函数，显示绕着旋转的轴：

这是6个全部的 a-b-a 轴旋转. 第一个是标准 z-y-z 欧拉旋转：

x-y-x 欧拉旋转：

x-z-x 欧拉旋转：

y-x-y 欧拉旋转：

y-z-y 欧拉旋转：

z-x-z 欧拉旋转：

然后是6个 a-b-c 轴旋转. 第一个是 x-y-z 欧拉旋转：

x-z-y 欧拉旋转：

y-x-z 欧拉旋转：

y-z-x 欧拉旋转：

z-x-y 欧拉旋转：

z-y-x 欧拉旋转：

平衡环架  (5)

平衡环架是由可旋转的环组成的系统，对象可以以任何方向自转. 它们用于各种导航和摄像应用：

平衡环架内的对象的方向可以使用 EulerMatrix 在圆环旋转角度下建模，从最外层到最里层的圆环. 注意使用 a-b-a 轴系统：

具有 a-b-c 轴旋转的平衡环架对初始状态为所有环的轴彼此垂直的平衡环系统建模：

这使用 z-y-x 欧拉旋转：

旋转系统可能进入平衡环架锁，这种情况下某角度值降低了系统的自由度. 正常的未锁住的情况产生下面的式子：

向量 {1,1,0} 可以旋转到曲面的任意一个点：

在锁住的情况下，只有差值 可以影响旋转：

目前，向量 {1,1,0} 只能旋转到曲线上的一个点：

当轴 时，平衡环架锁将出现，其中 . 下面的例子给出 x-y-x 旋转：

未锁住的 m1 和锁住的 m2 的情况：

z-y-z 旋转的未锁住 m1 和锁住 m2 的情况：

当轴全都不同 ，当 时出现平衡环架锁. 下面的例子给出 x-y-z 旋转：

锁住的 m1 和未锁住的 m2 情况：

y-x-z 旋转的锁住 m1 和未锁住的 m2 情况：

属性和关系  (11)

EulerMatrix 对应于三个旋转：

在普通的旋转轴排序下：

使用 EulerAngles 返回产生相同旋转矩阵的角度：

角度不必相同：

但是，两个角度集合产生相同的旋转矩阵：

使用 RollPitchYawMatrix 在每个步骤关于全局坐标框架旋转：

EulerMatrix 在每个步骤关于当前坐标框架旋转：

如果两个相邻的旋转轴相同，例如 或者 ，系统自由度为2，比如在执行 x-y-y 旋转时：

如果所有旋转轴是相同的话，例如 ，系统只有一个自由度，比如当执行 x-x-x 旋转时：

EulerMatrix[{α,β,γ},{a,b,c}] 与 RollPitchYawMatrix[{γ,β,α},{c,b,a}] 相同：

EulerMatrix 只应用于 ：

对于一般维度，使用 RotationMatrix：

EulerMatrix 关于三个轴方向的选择可参数化任何旋转：

对于一般轴旋转，使用 RotationMatrix：

EulerMatrix 是行列式为1的正交矩阵：

EulerMatrix 的逆是它的转置：

EulerMatrix[{α,β,γ}] 的逆是 EulerMatrix[{-γ,-β,-α}]:

EulerMatrix[{α,β,γ},{a,b,c}] 的逆是 EulerMatrix[{-γ,-β,-α},{c,b,a}]:

可能存在的问题  (1)

EulerMatrix 允许相等的相邻轴，而这产生一个旋转矩阵：

但是，EulerAngles 要求相邻轴不同：

这是因为在相邻轴相等的情况下，某些旋转矩阵无法表示：

巧妙范例  (1)

使用 GeometricTransformation 可视化一定范围角度内球面的旋转：

Wolfram Research (2015)，EulerMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EulerMatrix.html （更新于 2024 年）.

文本

Wolfram Research (2015)，EulerMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EulerMatrix.html （更新于 2024 年）.

CMS

Wolfram 语言. 2015. "EulerMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/EulerMatrix.html.

APA

Wolfram 语言. (2015). EulerMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/EulerMatrix.html 年

BibTeX

@misc{reference.wolfram_2024_eulermatrix, author="Wolfram Research", title="{EulerMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/EulerMatrix.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_eulermatrix, organization={Wolfram Research}, title={EulerMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/EulerMatrix.html}, note=[Accessed: 22-November-2024 ]}