Exists 
詳細

- Exists[x,expr]は
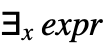 と入力できる.
と入力できる. 記号は
記号は ex
ex あるいは\[Exists]と入力できる.変数
あるいは\[Exists]と入力できる.変数 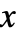 は下付き文字として与えられる.
は下付き文字として与えられる. - Exists[x,cond,expr]は
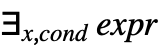 と入力できる.
と入力できる. - StandardFormでは,Exists[x,expr]は
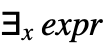 と出力される.
と出力される. - Exists[x,cond,expr]は
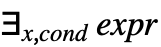 として出力される.
として出力される. - Existsは,Reduce,Resolve,FullSimplify等の関数で用いることができる.
- 制約条件 cond は,x∈Integersのように,しばしば変数の領域を指定するのに用いられる.
- Exists[x,cond,expr]はExists[x,cond&&expr]と等価である.
- Exists[{x1,x2,…},…]は
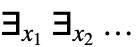 と等価である.
と等価である. - Exists[x,expr]における
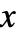 の値はBlockにおけるように局所化されると解釈される.
の値はBlockにおけるように局所化されると解釈される.
例題
すべて開くすべて閉じるスコープ (6)
アプリケーション (4)
次は,R1は満足するがR2は満足しない点があると述べている:
この陳述は偽である.したがってR1で定義された範囲はR2で定義された範囲に含まれる:
この陳述は真である.したがって推測は任意の三角形について真である訳ではない:
この陳述は偽である.したがってこの推測はすべての鋭角三角形について真である:
次は,この陳述が真ではない![]() の値は存在しないことを証明している:
の値は存在しないことを証明している:
これは,TautologyQを用いても証明できる:
特性と関係 (5)
Wolfram Research (2003), Exists, Wolfram言語関数, https://reference.wolfram.com/language/ref/Exists.html.
テキスト
Wolfram Research (2003), Exists, Wolfram言語関数, https://reference.wolfram.com/language/ref/Exists.html.
CMS
Wolfram Language. 2003. "Exists." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Exists.html.
APA
Wolfram Language. (2003). Exists. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Exists.html