FinancialBond
FinancialBond[params,ambientparams]
金融債権商品の値を与える.
FinancialBond[params,ambientparams,prop]
指定された特性 prop を計算する.
詳細とオプション




- FinancialBondは満期日の元金支払いと一連の利払いを含む金融商品クラスを表す.
- FinancialBondは数式あるいは任意の記号式に使うことができる.
- FinancialBond[params,ambientparams,{prop1,prop2,…}]は複数の特性を計算し結果をリストにして返す.
- FinancialBond[params,ambientparams,"Rules"]は使用可能な全特性を計算する.
- FinancialBondのパラメータはすべて規則の集合{param1,val1,param2,val2,…}]として与えられる.
- 使用可能なパラメータ
-
"FaceValue" 額面価格 "Coupon" 表面利率(支払い関数) "Maturity" 満期あるいはコール/プットの期日 "CouponInterval" 利払いの間隔 "RedemptionValue" 償還価値(額面と異なる場合) - 使用可能な環境パラメータ
-
"InterestRate" 最終利回りあるいは利回り "Settlement" 決済日 "DayCountBasis" 日数計算方法 - 決済日と満期の指定は日付あるいは抽象的な時間単位で入力することができる.
- 利払いは単一利率あるいは時間依存の支払い関数として指定することができる.
- 可能な利子指定
-
r 単一利回り {r1,r2,…} 単位時間間隔で適用される直物相場の表 {{t1,r1},{t2,r2},…} 指定時で変化する利率一覧 {p1->r1,p2->r2,…} 利率の期間構造 function 時間の関数として与えられる利力 - "DayCountBasis"に使える設定
-
"30/360" 米国債券ベース "30E/360" ユーロ債券ベース(ISDA 2006) "30E/360German" ユーロ債券ベース(ISDA 2000, ドイツ) "30E+/360" 30E+/360 日数計算方法 "ActualICMA" actual/actual ICMA "ActualISDA" actual/actual ISDA "Actual/365" actual/365 (固定) "Actual/360" actual/360 (フランス) "Actual/365L" actual/365L "ActualAFB" actual/actual AFB/FBF 基本契約 Automatic 精密な歴法算法 - FinancialBondで計算できる特性
-
"Value" 未収利息に対して調整された価格 "FullValue" 未調整価格 "AccruedInterest" 決算時の未収利息 "Duration" マコーレーデュレーション "ModifiedDuration" 修正デュレーション "Convexity" コンベクシティ "CouponPeriodDays" 決済日を含む利札期の日数 "CouponToSettlementDays" 直前の利払いから決済までの日数 "SettlementToCouponDays" 決済から次の利払いまでの日数 "NextCouponDate" 次の利札日 "PreviousCouponDate" 直前の利札日 "RemainingCoupons" 今後の利払い回数 "AccruedFactor" 未収利息を表す利払いの割合 - 満期が
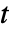 のFinancialBondで抽象的な時間単位が使われた場合,指定された決済日
のFinancialBondで抽象的な時間単位が使われた場合,指定された決済日 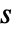 は債券の存在期間 (
は債券の存在期間 (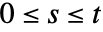 )内になければならない.
)内になければならない. - 慣例により,最終利回りと利払い指定は未調整で利息計算期間は利払い期間と等しいものとみなされる.EffectiveInterest関数あるいは関数的利率指定で所望する任意の利子計算が可能である.
- 利払い間隔 q が指定された場合,利払いは q, 2q, …に行われる.利払い間隔がなければ,支払いは1, 2, …に行われるものとみなされる."CouponInterval"->0と設定すると,"Coupon"->f で指定された関数は連続するものとみなされる.
- FinancialBondで日付が指定され,利払いあるいは利率のいずれかが関数として指定された場合,あるいは利率が率あるいは期間構造のリストとして指定された場合,関数は満期日からの年数の積分を表す決済日の直前の点に時間0があるものと仮定する.
- 支払い関数は循環関係として与えられることがある.FinancialBondで使えるように,RSolveを使って循環関係を時間の関数に変換することができる.
- FinancialBondで抽象的な時間単位が使われた場合,歴特性は適用できない.
- 使用可能なオプション
-
Assumptions $Assumptions パラメータについての仮定 GenerateConditions False パラメータについての条件を生成するかどうか
例題
すべて開くすべて閉じる例 (6)
スコープ (9)
FinancialBondは記号パラメータに使うことができ,閉形の式を求めることができる:
Apartを使って個別の支払いの割引係数を顕在化させることができる:
式を完全に分解するためにはApartを何回も適用する必要があるかもしれない:
FinancialBondを含む式の記号解を求めることができる:
支払い間隔として整数を使い.いくつかの区間で1回だけ発生する支払いを指定することができる:
FinancialBondに利率の期間構造あるいは将来の直物相場のリストを与えることができる:
時間によって変化する利率構造とともに日付が与えられた場合,時間0は満期からの年数の積分を表す決済日前の直近の点であるとみなされる.この場合は,時間0は2010年12月31日に当たる:
FinancialBondは利力とともに関数的( 成長)利札を取ることができる:
コンソール債券は満期日としてInfinity を使って評価することができる:
一般化と拡張 (5)
FinancialBondは名目利回りを取って利払い回数と同じ複利を仮定する.しかし,これとは異なる利息の元本組み入れ頻度を使うことが望ましい.EffectiveInterestを使うと利払い回数での複利の後の正しい有効割引率を与える利率を求めることができる:
Expectationを使って10年から15年の不定の期間に$1100で満期前償還が可能な額面価格$1000の債券の期待値を求めることができる:
EffectiveInterestを使って期間構造が与えられている場合にFinancialBondが使った実際の割引率を決定することができる:
RSolveを使って循環関係を時間だけの関数に変換することができる:
上記の循環関係は固定割合で1回ごとに額が上昇する支払いを表している.この解は時間のみの関数であり,FinancialBondで使うのに相応しい:
アプリケーション (7)
10年後に$1000の支払いで現在は$400で決済されるゼロクーポンがある.半年複利の黙示的利回りを求める:
10年もので額面$1000,期間1年の利札が付いたインフレ調整付き債券の値を求める.債券の当初表面利率は7%,各利札は先行するものより3%大きくなる.債券の償還価格は$1200である:
期間開始後3ヶ月で買われたと仮定して上記債券未収利息を求める:
5月1日に発行された 8%の半年利払いの額面$100,期間10年の債券がある.ほぼ2年後の5月15日にこの債券は$88で取引された.厳密な歴法算法を仮定してその日の利回りを求める:
償還価格$1200,コール日2020年12月31日,決済日2010年7月12日,期間半年のコーラブル債の価格:
満期2030年12月31日,決済日2013年9月5日の4%期間四半期の利付債の"30/360"日数計算方式を使った次の利払い日までの日数:
20年で半年利払いの利付債の当初利率は8%で価格は$1722.25である.この債券は15年目の終りから始めて任意の利払い日に額面でコールできる.6%の利回りを保証するための額面を求める:
これと同じ債券が額面1000,価格$1300だった場合,最低で7%の利回りを保証するための買入れ価格を求める:
この債券の価格が$900でコールが1100だった場合に投資家が望める最大利回り:
満期2030年12月31日,決済日2010年11月12日,期間半年の債券の""Actual/360"日数計算方式を使ったデュレーションとコンベクシティ:
特性と関係 (2)
デュレーションとコンベクシティは記号利回りと微分関数Dを使ってマニュアルで計算できる:
FinancialBond特性を使って同じ数量を計算する:
利払い期日に,FinancialBondオブジェクトの値は同じ支払い頻度で最終支払いが債券の額面に等しいAnnuityオブジェクトと同じ値を与える:
考えられる問題 (1)
債券は年金額と最終支払いによって定義することができるが,FinancialBondは価格を与えるのに対しTimeValueはAnnuityの時間価値に等しいものを返す.現在価値(時間0)の計算では違いはないが,0以外の時間を使った場合には違いが生まれる:
おもしろい例題 (2)
テキスト
Wolfram Research (2010), FinancialBond, Wolfram言語関数, https://reference.wolfram.com/language/ref/FinancialBond.html.
CMS
Wolfram Language. 2010. "FinancialBond." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FinancialBond.html.
APA
Wolfram Language. (2010). FinancialBond. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FinancialBond.html