FindEulerianCycle

FindEulerianCycle[g]

グラフ g のオイラー(Euler)閉路を求める．

FindEulerianCycle[g,k]

最高で k 個のオイラー閉路を求める．

FindEulerianCycle[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細

予備知識

  • FindEulerianCycleは，グラフ内の他と区別できる1つ以上のオイラー閉路（オイラー回路，オイラー路とも呼ばれる）を見付けようと試みる．閉路は，辺リストのリストとして，あるいは見付からない場合には{}として返される．オイラー閉路（閉路が特定の端点を持つ明示的な経路を使って識別される場合には，より正しくはオイラー回路と呼ばれる）は，最初と最後の辺が端点で繋がり，各辺が厳密に1度だけ現れるような，互いに区別の付く辺の連続する列である．オイラー閉路は，ゲノム配列を再構築したり，de Bruijn配列を構築したり，最適な学会のスケジューリングを求めたりするのに使える．
  • FindEulerianCycle[g,k]は，k 個のオイラー閉路を求めようと試みる．オイラー閉路では，回数指定 k を省略する（その場合には1であるとみなされる）場合も，正の整数の場合も，あるいはAllになる場合もある．オイラー閉路は，単純な閉路である必要はない．つまり，（必ず単純であるハミルトン(Hamilton)閉路とは違って）閉路内で頂点が繰り返されてもよい．
  • オイラー閉路を含むグラフはオイラーグラフと呼ばれる．ただし，「Euler」と「Eulerian」で使い分けて，つまり「Euler graph」ですべての頂点が偶次数であるグラフを指すとする場合もあるので注意が必要である．後者の定義は，連結した単純グラフは奇次数の頂点がない場合，かつその場合に限り，オイラー回路を持つというオイラーの正しい（彼自身によって証明されることはなかった）観察によるものである．オイラー閉路はこのため，ハミルトン(Hamiltonian)閉路よりも数学的に研究しやすい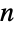． 個のノードを持つ連結したオイラー(Euler)グラフの数は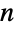， 個のノードを持つ連結したオイラー(Eulerian)グラフの数と等しいが，非連結のグラフについては数が異なる．どの閉路もすべての辺を通らないという場合でも，各ノードで複数の非連結の閉路を持つ非連結グラフが存在するからである．
  • EulerianGraphQは，グラフがオイラー(Eulerian)グラフであるかどうかを判断するのに使える．他の種類の閉路を見付けるための関数として，FindCycleとFindHamiltonianCycleがある．

例題

すべて開くすべて閉じる

例  (2)

オイラー閉路を求める：

オイラー閉路を示す：

複数のオイラー閉路を求める：

スコープ  (8)

FindEulerianCycleは無向グラフに使うことができる：

有向グラフ：

多重グラフ：

最高で3つのオイラー閉路を求める：

オイラー閉路を求める：

規則を使ってグラフを指定する：

FindEulerianCycleは非オイラーグラフに対しては空の結果を返す：

FindEulerianCycleは大きいグラフに使うことができる：

アプリケーション  (7)

ケーニヒスベルクのプレーゲル河に架かる7つの橋を2度通らずすべて1度だけ通ってもとの場所に戻ることはできない：

一筆書きで封筒の形をなぞる：

このグラフはオイラーグラフではない：

奇点が2つあるので（多重辺を避けるために）新たな頂点を通して奇点を繋いで拡張したオイラーグラフを作ることができる：

拡張したグラフの中でオイラー閉路を求める：

頂点 を含む辺が最後になるまでオイラー閉路の辺を回転させる：

オイラー路を示す：

以下の会議に最適な会議室のスケジュールを求める：

同じ会議への出席者を辺で結んだ出席者のグラフ：

1人が連続する2つの会議の両方に出席できるような最適のスケジュールはない：

出席者間の奇数の仮想会議を加える：

可能なスケジュール：

頂点が長さ(k-1)の部分配列で辺が長さ k の部分配列である，環状ゲノム"ATGGCGTGCA"のグラフに基づいたアセンブリ：

ゲノムを再構築する：

オイラー閉路から k 分木のde Bruijn系列を構築する：

de Bruijn系列：

有向オイラー閉路に沿って頂点が訪れられる順番を求める：

各辺のソース頂点を拾い出す：

オランダの風車グラフ(Dutch Windmill graph)のオイラーグラフを求める：

オイラー閉路に沿って訪れた辺にラベルを付ける：

特性と関係  (6)

オイラーグラフの大規模なコレクションを得るのにGraphDataを使う：

非オイラーグラフの大規模コレクションに使う：

EulerianGraphQを使ってグラフにオイラー閉路があるかどうか調べる：

頂点が偶次数の連結無向グラフにはオイラー閉路がある：

無向グラフが辺非連結オイラー閉路に分割できるとき，その無向グラフにはオイラー閉路がある：

無向オイラーグラフの線グラフにはオイラー閉路がある：

すべての頂点の入次数と出次数が等しい有向グラフにはオイラー閉路がある：

おもしろい例題  (1)

オイラー閉路を求める：

オイラー閉路を動的にハイライトする：

Wolfram Research (2010), FindEulerianCycle, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindEulerianCycle.html （2015年に更新）.

テキスト

Wolfram Research (2010), FindEulerianCycle, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindEulerianCycle.html （2015年に更新）.

CMS

Wolfram Language. 2010. "FindEulerianCycle." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/FindEulerianCycle.html.

APA

Wolfram Language. (2010). FindEulerianCycle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindEulerianCycle.html

BibTeX

@misc{reference.wolfram_2024_findeuleriancycle, author="Wolfram Research", title="{FindEulerianCycle}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FindEulerianCycle.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findeuleriancycle, organization={Wolfram Research}, title={FindEulerianCycle}, year={2015}, url={https://reference.wolfram.com/language/ref/FindEulerianCycle.html}, note=[Accessed: 18-November-2024 ]}