FindEulerianCycle

FindEulerianCycle[g]

求图 g 中的欧拉圈.

FindEulerianCycle[g,k]

求至多 k 个欧拉圈.

FindEulerianCycle[{vw,…},…]

使用规则 vw 指定图 g.

更多信息

背景

  • FindEulerianCycle 试图找出一个或多个不同的欧拉圈，也被称为图的欧拉环路，欧拉巡回或欧拉回路. 欧拉圈会作为边列表的列表返回，不存在时则返回 {}. 欧拉圈（若该圈被显式路径标明且路径由特定端点组成，则更适合被称为环路）是由不同边组成的一个连续序列，头尾两条边的端点是重合的且图的每条边都恰好出现一次. 欧拉圈可被用于重建基因组序列，构建 de Bruijin 序列，以及寻找最佳会议排期.
  • FindEulerianCycle[g,k] 试图找出 k 个欧拉圈，其中计数要求 k 可以被省略（在这种情况下它取值为 1），或者也可以设为 All. 欧拉圈不必是简单圈，即圈中可以有重复的顶点（不像哈密尔顿圈，它总是简单的）.
  • 具有欧拉圈的图被称为欧拉图. 然而，这里需要谨慎的解释一下术语，因为有些作者把欧拉图定义为另一种东西，用来命名所有顶点都是偶数度的图. 后一定义是受欧拉的正确（但不是他证明的）观察启发，他注意到连通简单图有欧拉回路当且仅当没有一个顶点是奇数度的. 欧拉圈因此在数学上比哈密尔顿圈要容易研究些. 尽管连通情况下有 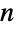个结点的两种欧拉图数量是一样的，但不连通情况下数量就不一样了，因为存在不连通的图具有多个不连通的圈，它的每个结点都是偶数度的但没有单个的圈可以经过所有的边.
  • EulerianGraphQ 可被用于判定一个图是不是欧拉图. 寻找其它类型的圈的函数包括 FindCycle 和 FindHamiltonianCycle.

范例

打开所有单元关闭所有单元

基本范例  (2)

求欧拉圈：

显示欧拉圈：

求若干个欧拉圈：

范围  (8)

FindEulerianCycle 可用于无向图：

有向图：

多重图：

求若干个欧拉圈：

求所有的欧拉圈：

使用规则指定图：

FindEulerianCycle 对于非欧拉图返回空结果：

FindEulerianCycle 可用于大规模图：

应用  (7)

普雷格尔河上柯尼斯堡市的七座桥不能无重复的由单条路径遍历，尤其还要求在和起点相同的地方结束行程：

描绘出一个信封的图案，并且无需抬起钢笔，无需两次划过同一条线：

该图不是欧拉图：

由于存在两个度数为奇数的顶点，通过经由一个新的顶点（以避免多重边）连接度数为奇数的顶点，可构建增广欧拉图：

在增广图中，找到一个欧拉圈：

对回路内的边进行轮转，直到含有顶点 的边成为最后的几条边：

显示欧拉路径：

求以下会议的会议室的最佳安排：

由参加者组成的图，其中的边连接参加相同会议的参加者：

没有最优的会议安排，能使得连续的两次会议共享一个参加者：

在具有奇数会议次数的参加者之间添加虚拟会议：

一种可能的安排：

由圆形基因组 "ATGGCGTGCA" 组成的基于图的组合，其中顶点作为 (k-1) 部，而边作为 k 部：

重建基因组：

从欧拉圈构建 k 重 de Bruijn 序列：

De Bruijn 序列：

求沿着有向圈的顶点顺序：

挑出每条边的起始顶点：

求荷兰风车图的欧拉圈：

沿着欧拉圈对边添加标签：

属性和关系  (6)

对大量欧拉图集合使用 GraphData：

非欧拉图：

利用 EulerianGraphQ 检验一个图是否含有欧拉圈：

一个顶点都是偶数度的连通无向图才含有欧拉圈：

如果一个无向图可以被分解为边互不相交的圈，则该图含有欧拉圈：

一个无向欧拉图的线图含有欧拉圈：

当且仅当每个顶点具有相等的入度和出度时，一个有向图才含有欧拉圈：

巧妙范例  (1)

求欧拉圈：

动态突出显示圈：

Wolfram Research (2010)，FindEulerianCycle，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FindEulerianCycle.html （更新于 2015 年）.

文本

Wolfram Research (2010)，FindEulerianCycle，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FindEulerianCycle.html （更新于 2015 年）.

CMS

Wolfram 语言. 2010. "FindEulerianCycle." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/FindEulerianCycle.html.

APA

Wolfram 语言. (2010). FindEulerianCycle. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FindEulerianCycle.html 年

BibTeX

@misc{reference.wolfram_2024_findeuleriancycle, author="Wolfram Research", title="{FindEulerianCycle}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FindEulerianCycle.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findeuleriancycle, organization={Wolfram Research}, title={FindEulerianCycle}, year={2015}, url={https://reference.wolfram.com/language/ref/FindEulerianCycle.html}, note=[Accessed: 18-November-2024 ]}