FindGraphIsomorphism

✖

FindGraphIsomorphism[g₁,g₂]

finds an isomorphism that maps the graph g₁ to g₂ by renaming vertices.

✖

FindGraphIsomorphism[g₁,g₂,n]

finds at most n isomorphisms.

✖

FindGraphIsomorphism[{vw,…},…]

uses rules vw to specify the graph g.

Details and Options

FindGraphIsomorphism is also known as edge-preserving bijection.
FindGraphIsomorphism is typically used for identification of equivalent structures and verification of equivalence of various representations.

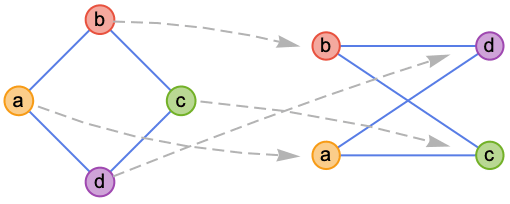
FindGraphIsomorphism gives a list of associations Association[v₁->w₁,v₂->w₂,…] such that v_i and v_j are adjacent vertices in g₁ if w_i and w_j are adjacent vertices in g₂, and vice versa.
FindGraphIsomorphism gives an empty list if no isomorphism can be found.
FindGraphIsomorphism[g₁,g₂,All] gives all the isomorphisms.

Examples

open allclose all

Basic Examples (2)Summary of the most common use cases

Find an isomorphism that maps two graphs:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-f5edt

Out[1]=1

Find all isomorphisms:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-guputi

Out[1]=1

Scope (8)Survey of the scope of standard use cases

Specification (5)

FindGraphIsomorphism works with undirected graphs:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-d9n8ou

Out[1]=1

Directed graphs:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-bjwckj

Out[1]=1

Use rules to specify the graph:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-bndh30

Out[1]=1

It returns an empty list if no isomorphism can be found:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-b83ts

Out[1]=1

FindGraphIsomorphism works with large graphs:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-fl62op

In[2]:=2

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-hx93y

In[3]:=3

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-4iugm

Out[3]=3

Enumeration (3)

Find an isomorphism that maps two graphs:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-cvsbaj

Out[1]=1

Find at most two isomorphisms:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-j7b3rh

Out[1]=1

Find all isomorphisms:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-kewkuy

Out[1]=1

Applications (1)Sample problems that can be solved with this function

Find an isomorphism that maps two graphs:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-cmg60p

In[2]:=2

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-hyregk

In[3]:=3

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-cvr7dg

In[4]:=4

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-nagfe

In[5]:=5

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-da11ma

Out[5]=5

Highlight and label two graphs according to the mapping:

In[6]:=6

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-bc8hxs

In[7]:=7

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-frhw52

In[8]:=8

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-g2k4x2

Out[8]=8

Properties & Relations (3)Properties of the function, and connections to other functions

Isomorphic graphs have the same number of vertices and edges:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-baigi

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-c1suyl

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-subr3

Out[3]=3

In[4]:=4

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-ch2vsv

Out[4]=4

Test whether two graphs are isomorphic using IsomorphicGraphQ:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-f4vgcx

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-fw1rxe

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-b8ah4f

Out[3]=3

Isomorphic graphs have the same canonical graph:

In[1]:=1

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-gawxbw

In[2]:=2

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-bzde4x

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0rkgdpvtjbdtg14-bbygwo

Out[3]=3

Top