FindIndependentVertexSet

FindIndependentVertexSet[g]

求图 g 的具有最大顶点数的独立顶点集.

FindIndependentVertexSet[g,n]

求至多有 n 个顶点的独立顶点集.

FindIndependentVertexSet[g,{n}]

求恰好具有 n 个顶点的独立顶点集.

FindIndependentVertexSet[g,{nmin,nmax}]

求所含顶点数在 nmin 和 nmax 之间的独立顶点集.

FindIndependentVertexSet[g,nspec,s]

求至多 s 个独立顶点集.

FindIndependentVertexSet[{g,v},…]

求仅包含顶点 v 的独立集.

FindIndependentVertexSet[{vw,…},…]

使用规则 vw 指定图 g.

更多信息

背景

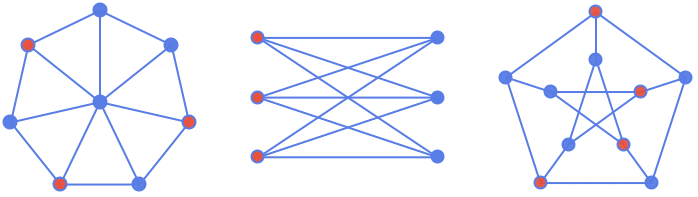
  • FindIndependentVertexSet 会找出图中的一个或更多的极大独立顶点集，以顶点列表的列表形式返回. 这里，独立顶点集是一个顶点集合，此集合中任意两个顶点之间都没有边相连. 独立顶点集在金融、编码理论、地图标注、模式识别、社交网络、分子生物学和调度方面都有应用.
  • 有两种特别重要的独立顶点集：最大独立集和极大独立集. 要注意这两种并不等价. 最大独立顶点集是包含给定图的最多顶点的独立集. 与之相反，极大独立顶点集是无法再添加相邻顶点的顶点集，这意味着它不是更大的独立顶点集的子集. 最大独立顶点集因此总是极大的，反之则未必成立.
  • FindIndependentVertexSet 能找到不同大小的极大独立顶点集. FindIndependentVertexSet 也能找到指定大小的单个极大独立顶点集，指定数量的极大独立顶点集，或所有这样的集合.
  • FindIndependentVertexSet[g] 能找出图 g 的单个最大独立顶点集，FindIndependentVertexSet[g,Length/@FindIndependentVertexSet[g],s] 能找出最多有 s 个顶点的，而 FindIndependentVertexSet[g,Length/@FindIndependentVertexSet[g],All] 能找出全部这样的集合. 图 g 的最大独立顶点集的大小被称为其（顶点）独立数. 找出给定图的最大独立顶点集（以及由此可得的独立数）这一问题是 NP 完全的，这意味着计算会极其慢.
  • FindIndependentVertexSet[g,Infinity] 能找出图 g 的单个极大独立顶点集，FindIndependentVertexSet[g,Infinity,s] 能找出最多 s 个顶点集，而 FindIndependentVertexSet[g,Infinity,All] 能找出全部这样的集合.
  • 不一定极大的独立顶点集不能用 FindIndependentVertexSet 直接求得，但可通过对所有极大独立顶点集的所有子集求并集以简单枚举出来.
  • 可以用 IndependentVertexSetQ 检测一个顶点集是不是独立的（不需要它还是极大的）. 独立顶点集对应的是顶点覆盖的补集（和 FindVertexCover 比较）. 极大独立顶点集等价于 GraphComplement 上的极大团（和 FindClique 比较）. FindIndependentEdgeSet 将与 FindIndependentVertexSet 相同的概念应用到边上，得到的独立边集也被称为“匹配”.

范例

打开所有单元关闭所有单元

基本范例  (2)

求图的独立顶点集：

显示顶点集：

求所有独立集：

范围  (14)

FindIndependentVertexSet 适用于无向图：

有向图：

加权图：

多重图：

混合图：

求最大的独立顶点集：

恰好有3个顶点的独立顶点集：

含有最多2个顶点的独立顶点集：

顶点数在3到5之间的独立顶点集：

含有给定顶点的最大独立顶点集：

求图的所有独立顶点集：

使用规则指定图：

如果没有独立顶点集，FindIndependentVertexSet 会给出一个空列表：

FindIndependentVertexSet 适用于大型图：

应用  (3)

突出显示图的所有独立顶点集：

在一个特许经营服务网络中，顶点是店铺位置，如果两家店距离太近以致干扰销量，则是相连的. 有一家商店在 NorthPoint，求新店铺的可能位置：

新店铺的可能位置：

求道琼斯工业指数中回报不是高度相关的成员：

首先计算自今年年初以来回报率的相关性：

建立一个图，边由相关性系数大于选定的 theta 的股票连接构成：

股票不高度相关的一个最大组：

属性和关系  (4)

使用 IndependentVertexSetQ，检验一个顶点集是否为独立顶点集：

独立顶点集的补集是顶点覆盖集：

由独立顶点集给出的子补图是完全图：

二分图具有等长度的边覆盖和独立顶点集：

Wolfram Research (2010)，FindIndependentVertexSet，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FindIndependentVertexSet.html （更新于 2015 年）.

文本

Wolfram Research (2010)，FindIndependentVertexSet，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FindIndependentVertexSet.html （更新于 2015 年）.

CMS

Wolfram 语言. 2010. "FindIndependentVertexSet." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/FindIndependentVertexSet.html.

APA

Wolfram 语言. (2010). FindIndependentVertexSet. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FindIndependentVertexSet.html 年

BibTeX

@misc{reference.wolfram_2024_findindependentvertexset, author="Wolfram Research", title="{FindIndependentVertexSet}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FindIndependentVertexSet.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findindependentvertexset, organization={Wolfram Research}, title={FindIndependentVertexSet}, year={2015}, url={https://reference.wolfram.com/language/ref/FindIndependentVertexSet.html}, note=[Accessed: 18-November-2024 ]}