WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

GraphComplement
✖
GraphComplement

✖

gives the graph complement of the graph g.

✖
GraphComplement[{vw,…}]

uses rules vw to specify the graph g.

Details and Options

  • GraphComplement is also known as edge-complementary graph.
  • The graph complement has the same vertices and edges defined by two vertices being adjacent only if they are not adjacent in g.
  • GraphComplement works with undirected graphs, directed graphs, multigraphs, and mixed graphs.

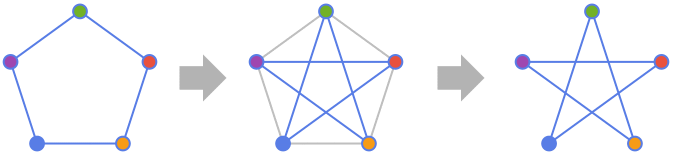
Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

Graph complement of cycle graphs:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-b1kkxi
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b8dvz1cr2-b3rg0e
Out[2]=2

Graph complement of directed graphs:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-e4hi6a
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b8dvz1cr2-clnng3
Out[2]=2

Scope  (6)Survey of the scope of standard use cases

GraphComplement works with undirected graphs:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-n26fy
Out[1]=1

Directed graphs:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-i3p7rw
Out[1]=1

Multiple graphs:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-djehuq
Out[1]=1

Mixed graphs:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-czvddh
Out[1]=1

Use rules to specify the graph:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-bndh30
Out[1]=1

GraphComplement works with large graphs:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-ejnwgv
In[2]:=2
✖
https://wolfram.com/xid/0b8dvz1cr2-wogg5a
Out[2]=2

Properties & Relations  (7)Properties of the function, and connections to other functions

The complement of a CompleteGraph is an edgeless graph:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-s8par
Out[1]=1

The complement of the complement is the original graph (for simple graphs):

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-dfpcpm
Out[1]=1

The complement of the graph can be obtained from its adjacency matrix:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-ck85j2
In[2]:=2
✖
https://wolfram.com/xid/0b8dvz1cr2-ctd3le
In[3]:=3
✖
https://wolfram.com/xid/0b8dvz1cr2-g3wjcf
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0b8dvz1cr2-bnzbl2
Out[4]=4

An independent vertex set of the graph is a clique of its complement graph:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-k0rgt4
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b8dvz1cr2-ggrswc
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0b8dvz1cr2-zo19z
Out[3]=3

The complement of the line graph of is a Petersen graph:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-g8s4u4
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b8dvz1cr2-k80ax
Out[2]=2

The graph union of any simple graph and its complement is a complete graph:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-hch6zr
In[2]:=2
✖
https://wolfram.com/xid/0b8dvz1cr2-emajil
Out[2]=2

The graph intersection of any graph and its complement is an empty graph:

In[1]:=1
✖
https://wolfram.com/xid/0b8dvz1cr2-b1mhiw
In[2]:=2
✖
https://wolfram.com/xid/0b8dvz1cr2-b5yq85
Out[2]=2
Wolfram Research (2010), GraphComplement, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphComplement.html (updated 2015).
✖
Wolfram Research (2010), GraphComplement, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphComplement.html (updated 2015).

Text

Wolfram Research (2010), GraphComplement, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphComplement.html (updated 2015).

✖
Wolfram Research (2010), GraphComplement, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphComplement.html (updated 2015).

CMS

Wolfram Language. 2010. "GraphComplement." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphComplement.html.

✖
Wolfram Language. 2010. "GraphComplement." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphComplement.html.

APA

Wolfram Language. (2010). GraphComplement. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphComplement.html

✖
Wolfram Language. (2010). GraphComplement. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphComplement.html

BibTeX

@misc{reference.wolfram_2025_graphcomplement, author="Wolfram Research", title="{GraphComplement}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphComplement.html}", note=[Accessed: 17-May-2025 ]}

✖
@misc{reference.wolfram_2025_graphcomplement, author="Wolfram Research", title="{GraphComplement}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphComplement.html}", note=[Accessed: 17-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_graphcomplement, organization={Wolfram Research}, title={GraphComplement}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphComplement.html}, note=[Accessed: 17-May-2025 ]}

✖
@online{reference.wolfram_2025_graphcomplement, organization={Wolfram Research}, title={GraphComplement}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphComplement.html}, note=[Accessed: 17-May-2025 ]}