FindIntegerNullVector

FindIntegerNullVector[{x1,x2,…,xn}]

であるような整数 のリストを求める．

FindIntegerNullVector[{x1,x2,…,xn},d]

であるようなTemplateBox[{{{, {{a, _, 1}, ,, ..., ,, {a, _, n}}, }}}, Norm]<=d の整数 のリストを求める．

詳細とオプション

  • FindIntegerNullVectorは，PSLQあるいは番号識別としても知られている．
  • すべての aiが0である訳ではない．数 xiは実数でも複素数でもよい．複素数 xiについては，数 aiはガウス整数である．
  • FindIntegerNullVector[{x1,x2,…},d]では，指定されたノルム境界では整数零ベクトルは存在しないかもしれない．その場合，入力は未評価で返される．
  • 指定可能なオプション
  • WorkingPrecision Automatic内部計算で使う精度
    ZeroTest Automatic数が0であるかどうかをテストするメソッド
  • ZeroTest->Automaticと設定すると整数関係 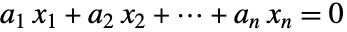をテストするメソッドが自動的に決められる．
  • 非厳密数 xiについては，求まった関係は入力の精度まで正しい．厳密数 xi については，求まった関係はPossibleZeroQを使って証明される．
  • 非厳密数 xiでWorkingPrecision->Automaticの場合，精度は入力精度であると解釈される．
  • 厳密数 xiでWorkingPrecision->Automaticの場合，精度はMachinePrecisionから始まってノルム境界 d が指定されていない場合に整数零ベクトルを求める場合には$MaxExtraPrecisionまで使われると考えられる．ノルム境界 d が定まっている場合には，零ベクトルを求めるかあるいは零ベクトルが存在しないことを証明するために十分な精度が使われる．

例題

すべて開くすべて閉じる

例  (3)

厳密入力：

厳密ではない入力：

ノルム境界を有する厳密入力：

2以下のノルムには零ベクトルがない：

スコープ  (6)

次は，厳密な有理数のベクトルの整数零ベクトルを求める：

次は，8以下のノルムでは零ベクトルがないことを証明している：

零ベクトルのノルム近くの境界では，零ベクトルが存在しないことが証明できないことがある：

返された零ベクトルはノルム境界を満足しない：

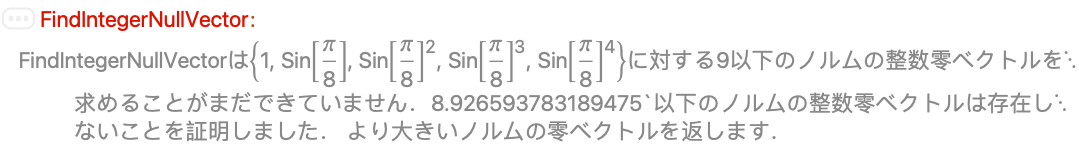
FindIntegerNullVectorは数が整数上で線形非依存であることは証明できない：

次は与えられれた境界以下では整数零ベクトルがないことを証明している：

厳密ではない入力の場合，関係は入力精度まで真である：

与えられたノルム境界では零ベクトルは存在しない：

次では零ベクトルは求まらないが，零ベクトルが存在しないことは小さいノルム境界についてしか証明されない：

次は の20桁精度近似で零ベクトルを求める：

厳密ベクトル については結果は零ベクトルではない：

のより高精度の近似で求まった零ベクトルは厳密ベクトル についても零ベクトルである：

これは厳密な複素数ベクトルのガウス整数零ベクトルを与える：

これは近似複素数ベクトルのガウス整数零ベクトルを求める：

オプション  (2)

WorkingPrecision  (1)

デフォルトで，最高$MachinePrecision+$MaxExtraPrecision桁の精度が使われる：

より高いWorkingPrecisionを使うと零ベクトルが求まる：

ZeroTest  (1)

デフォルトで，関係の証明にはMethod->"ExactAlgebraics"のPossibleZeroQが使われる：

次は，厳密メソッドを使って関係を証明する：

次は，代りに高精度数値テストを使う：

アプリケーション  (3)

代数的数の最小多項式の係数を求める：

次は，記号メソッドで最小多項式を求める：

超越数間の関係を求める：

の近似値を計算するMachinの公式の係数を求める：

特性と関係  (3)

FindIntegerNullVectorは指定されたベクトルの整数零ベクトルを返す：

整数零ベクトルは同次線形方程式の自明ではない整数解である：

FindInstanceを使って方程式の解を求める：

近似を使って代数的数の最小多項式の係数を求める：

RootApproximantを使って代数的数をその近似から求める：

考えられる問題  (2)

数の間の関係を求めるためには近似精度が十分ではないかもしれない：

より高い精度で近似を行うと真の関係が得られる：

非代数的数に対しての数値的なゼロテストは零ベクトルではない結果も許容する：

次は記号的ゼロテストメソッドがどれも適用されない場合にゼロテストに使われた精度を与える：

ゼロテストの精度をより高くすると，FindIntegerNullVectorはベクトルを正しく棄却する：

システムオプションをもとの値にリセットする：

Wolfram Research (2010), FindIntegerNullVector, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindIntegerNullVector.html.

テキスト

Wolfram Research (2010), FindIntegerNullVector, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindIntegerNullVector.html.

CMS

Wolfram Language. 2010. "FindIntegerNullVector." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FindIntegerNullVector.html.

APA

Wolfram Language. (2010). FindIntegerNullVector. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindIntegerNullVector.html

BibTeX

@misc{reference.wolfram_2024_findintegernullvector, author="Wolfram Research", title="{FindIntegerNullVector}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/FindIntegerNullVector.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findintegernullvector, organization={Wolfram Research}, title={FindIntegerNullVector}, year={2010}, url={https://reference.wolfram.com/language/ref/FindIntegerNullVector.html}, note=[Accessed: 18-November-2024 ]}