PossibleZeroQ

PossibleZeroQ[expr]

gives True if basic symbolic and numerical methods suggest that expr has value zero, and gives False otherwise.

Details and Options

  • The general problem of determining whether an expression has value zero is undecidable; PossibleZeroQ provides a quick but not always accurate test.
  • With the setting Method->"ExactAlgebraics", PossibleZeroQ will use exact guaranteed methods in the case of explicit algebraic numbers.

Examples

open allclose all

Basic Examples  (1)

Test whether a numeric expression is zero:

Test whether a symbolic expression is likely to be identically zero:

Scope  (4)

Show that a numeric expression is zero:

Show that a numeric expression is nonzero:

Decide that a numeric expression is zero based on approximate computations:

Test whether symbolic expressions are likely to be identically zero:

Options  (2)

Assumptions  (1)

For arbitrary complex x, f is not identically zero:

When Re[x]>0, f is identically zero:

Method  (1)

By default, numeric approximations may be used to decide that an algebraic number is zero:

Approximate methods may give incorrect positive answers:

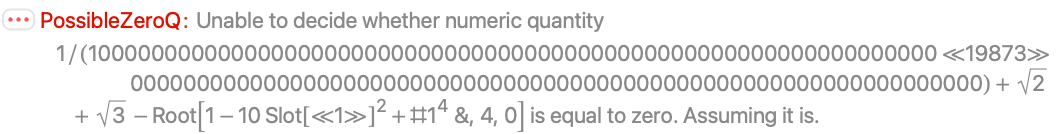
With Method->"ExactAlgebraics" exact methods are used for explicit algebraic numbers:

For explicit algebraic numbers the answer is provably correct:

Applications  (1)

Solving polynomial equations requires deciding whether coefficients are zero:

Wolfram Language equation solvers use zero testing automatically:

Properties & Relations  (1)

SameQ[e,0] returns True only if e is explicitly identical to zero:

Equal[e,0] uses simple tests to decide whether e is zero:

When Equal cannot decide whether an expression is zero it returns unchanged:

PossibleZeroQ uses numeric methods to test whether ee is zero:

FullSimplify proves symbolically that ee is zero:

Possible Issues  (1)

PossibleZeroQ may return True for nonzero numeric expressions that are close to zero:

Wolfram Research (2007), PossibleZeroQ, Wolfram Language function, https://reference.wolfram.com/language/ref/PossibleZeroQ.html.

Text

Wolfram Research (2007), PossibleZeroQ, Wolfram Language function, https://reference.wolfram.com/language/ref/PossibleZeroQ.html.

CMS

Wolfram Language. 2007. "PossibleZeroQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PossibleZeroQ.html.

APA

Wolfram Language. (2007). PossibleZeroQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PossibleZeroQ.html

BibTeX

@misc{reference.wolfram_2025_possiblezeroq, author="Wolfram Research", title="{PossibleZeroQ}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/PossibleZeroQ.html}", note=[Accessed: 24-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_possiblezeroq, organization={Wolfram Research}, title={PossibleZeroQ}, year={2007}, url={https://reference.wolfram.com/language/ref/PossibleZeroQ.html}, note=[Accessed: 24-April-2025 ]}