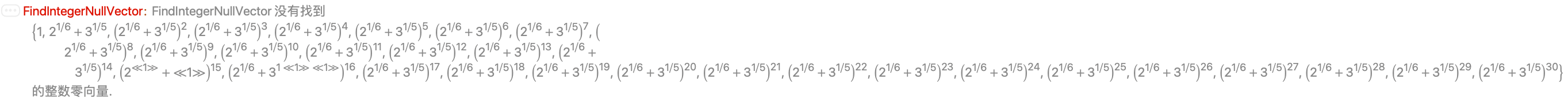FindIntegerNullVector

FindIntegerNullVector[{x1,x2,…,xn}]

找出整数 的列表，以使得 .

FindIntegerNullVector[{x1,x2,…,xn},d]

找出满足 TemplateBox[{{{, {{a, _, 1}, ,, ..., ,, {a, _, n}}, }}}, Norm]<=d 的整数 的列表，以使得 .

更多信息和选项

  • FindIntegerNullVector 亦称为 PSLQ 或数字识别.
  • 不是所有的 ai 都是零. 数字 xi 可以是实数或者复数. 对于复数 xi，数字 ai 是高斯整数.
  • 在 FindIntegerNullVector[{x1,x2,…},d] 中，对于给定的范数界限，整数零向量有可能不存在. 这种情况下返回的是未计算的输入的形式.
  • 可以有如下选项：
  • WorkingPrecision Automatic内部计算所用的精度
    ZeroTest Automatic用于检验一个数是否为零的方法
  • 设置 ZeroTest->Automatic 自动确定检验整数关系 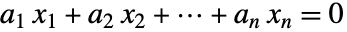的方法.
  • 对于非精确数 xi，所求得的关系在输入的精度下成立. 对于精确数 xi，所求得的关系利用 PossibleZeroQ 验证.
  • 对于非精确数 xi 和 WorkingPrecision->Automatic 设置，精度采用的是输入的精度.
  • 对于精确数 xi 和 WorkingPrecision->Automatic 设置，在没有指定范数界限 d 情况下搜索一个整数零向量时，精度将从 MachinePrecision 开始并使用至多为 $MaxExtraPrecision 的额外精度. 在给定范数界限 d 的情况下，则使用足够的精度寻找零向量或证明不存在零向量.

范例

打开所有单元关闭所有单元

基本范例  (3)

精确输入：

非精确输入：

具有范数界限的精确输入：

不存在范数小于或者等于2的零向量：

范围  (6)

下面求精确实数向量的整数零向量：

下面证明不存在范数少于或者等于8的零向量：

对于一个与零向量的范数接近的界限，您可能无法得到零向量不存在的证明：

所返回的零向量不满足范数界限：

FindIntegerNullVector 不能证明在整数范围内数字是线性独立的：

它可以证明不存在范数小于或者等于给定界限的整数零向量：

对于非精确输入，在输入精度范围内，关系为真：

对给定的范数界限，不存在零向量：

下面没有找到零向量，但是仅对较小的范数界限证明了零向量的不存在：

下面求 的20位近似的一个零向量：

结果不是精确向量 的一个零向量：

针对 的较高精度的近似所求得的一个零向量也是 的一个零向量：

下面给出精确复数组成的向量的一个高斯整数零向量：

下面求近似复数组成的向量的高斯整数零向量：

选项  (2)

WorkingPrecision  (1)

默认情况下，使用的精度至多有 $MachinePrecision+$MaxExtraPrecision 个数位：

使用较高的 WorkingPrecision 可帮助您找到一个零向量：

ZeroTest  (1)

默认情况下，带有 Method->"ExactAlgebraics" 的 PossibleZeroQ 用于证明某些关系：

下面使用精确方法证明该关系：

下面用的是高精度数值检验：

应用  (3)

求一个代数数的最小多项式的系数：

使用符号式方法求最小多项式：

求超越数之间的关系：

求 Machin 公式中计算 近似值的系数：

属性和关系  (3)

对给定的向量，FindIntegerNullVector 返回一个整数零向量：

整数零向量是齐次线性方程的一个非平凡整数解：

使用 FindInstance 求方程的解：

利用代数数的近似值求其最小多项式的系数：

利用 RootApproximant 使用其近似值求一个代数数：

可能存在的问题  (2)

近似的精度可能不足以求得数值之间的关系：

利用较高精度的近似，您可以得到一个正确的关系：

用于非代数数的数值式零检验方法可能允许产生并非零向量的结果：

下面给出在没有应用符号式零检验方法时，零检验中使用的精度：

在较高的零检验精度下，FindIntegerNullVector 准确地拒绝了该向量：

把系统选项设为初始值：

Wolfram Research (2010)，FindIntegerNullVector，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FindIntegerNullVector.html.

文本

Wolfram Research (2010)，FindIntegerNullVector，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FindIntegerNullVector.html.

CMS

Wolfram 语言. 2010. "FindIntegerNullVector." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FindIntegerNullVector.html.

APA

Wolfram 语言. (2010). FindIntegerNullVector. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FindIntegerNullVector.html 年

BibTeX

@misc{reference.wolfram_2024_findintegernullvector, author="Wolfram Research", title="{FindIntegerNullVector}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/FindIntegerNullVector.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findintegernullvector, organization={Wolfram Research}, title={FindIntegerNullVector}, year={2010}, url={https://reference.wolfram.com/language/ref/FindIntegerNullVector.html}, note=[Accessed: 18-November-2024 ]}