WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

FindRoot

FindRoot[f,{x,x₀}]

x=x₀ から始めて f の数値根を求める．

FindRoot[lhs==rhs,{x,x₀}]

方程式 lhs==rhs の数値解を求める．

FindRoot[{f₁,f₂,…},{{x,x₀},{y,y₀},…}]

すべての f_i の連立数値根を求める．

FindRoot[{eqn₁,eqn₂,…},{{x,x₀},{y,y₀},…}]

連立方程式 eqn_iの数値解を求める．

詳細とオプション

変数の初期値がリストで与えられているとき，変数の値は同じ次元のリストであると解釈される．
FindRootはSolveから得るのと同じ形式の x, y, … のための代入リストを返す．
FindRootは，まずすべての変数の値を局所化し，次に記号的となった変数で f を評価し，繰り返して結果を数値的に評価する．
FindRootは属性HoldAllを持ち，Blockを用いて実質的に変数を局所化する．
FindRoot[lhs==rhs,{x,x₀,x₁}]は x₀と x₁を x の最初の2つの値とし，導関数を用いずに解を求める．
FindRoot[lhs==rhs,{x,x_start,x_min,x_max}]は，x が x_minから x_maxの範囲外に出た場合にこの検索を中止するという条件で，解を求める．
x の初期値を1つしか指定しなければ，FindRootはニュートン法を用いて解を求める．初期値を2つ指定すると，FindRootは割線法の変形を用いる．
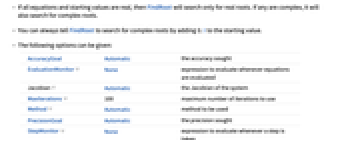
すべての方程式と初期値が実数の場合，FindRootは実根のみを求める．複素数が含まれる場合は複素根も求める．
初期値に0.Iを加えることで，常にFindRootに複素根を求めさせることができる．
指定可能なオプション

	AccuracyGoal	Automatic	目標とする確度
	EvaluationMonitor	None	式が評価されたときに常に評価される式
	Jacobian	Automatic	この系のヤコビ行列式
	MaxIterations	100	使用する最大反復回数
		Automatic	使用するメソッド
	PrecisionGoal	Automatic	目標とする精度
	StepMonitor	None	ステップを取るたびに常に評価される式
	WorkingPrecision	MachinePrecision	内部計算に使用する精度

デフォルト設定ではAccuracyGoalとPrecisionGoalの設定はWorkingPrecision/2である．
AccuracyGoalの設定で，根の位置の値と根における関数の値の両方の目標確度の桁数を指定する．
PrecisionGoalの設定で根の位置の値の目標精度桁数を指定する．
FindRootはAccuracyGoalまたはPrecisionGoalで指定された目標精度（または確度）に達するまで計算を続ける．
FindRootがMaxIterationsの反復ステップ内で指定された正確さの解が見出せない場合，最近見出した近似解を返す．この場合，この点を初期値としてFindRootを再適用する．

例題

すべて開くすべて閉じる

例 (3)

付近での根を求める：

付近での解を求める：

非線形方程式系を解く：

スコープ (4)

2つの非線形方程式の系の解を求める：

三変数の三変成分関数の根を求める：

複素数の初期値を与えることで複素数値を使った探索が行える：

実数入力に対して方程式が複素数である場合，実数の初期値が複素数の結果を与えていることがある：

一般化と拡張 (1)

変数は，初期値で指定されている場合にはベクトル値として考えることができる：

オプション (9)

AccuracyGoalとPrecisionGoal (1)

誤差推定の許容率を変える：

停止のために誤差許容率を緩める：

根までの推定相対距離を停止の主要基準とする：

DampingFactor (1)

DampingFactorを使って高次根への収束をスピードアップすることができる：

EvaluationMonitor (1)

EvaluationMonitorを使って使用された関数評価を追跡記録することができる：

Jacobian (1)

「ブラックボックス」関数に関数行列式を指定する：

指定された関数行列式がなければ，有限差分の計算に余分な評価が行われる：

疎な形式を知っているならば，疎なパターンテンプレートを指定することで評価回数を少なくできる：

さまざまなメソッドが必要とするヤコビ行列式の評価数を調べる：

MaxIterations (1)

使うステップ数を制限したり増したりする：

デフォルトの反復回数は100である：

この軟化子関数はにおいてすべての導関数が0なので，アルゴリズムは最終的に停止する：

Method (2)

メソッドオプションについては制約条件のない最適化も参照されたい．

異なる方法での根を求める：

FindRootで使われるステップと評価をモニターする関数を定義する：

デフォルトの方法（ニュートン法）：

ブレント(Brent)法の根の囲い込みには根を囲む2つの初期条件が必要である：

割線法は2つの初期条件で始まる：

アフィン共変ニュートン法を選択する：

StepMonitor (1)

いつ反復ステップが取られるかモニターする：

の等高線プロット上でステップを表す：

ステップ（赤）とその評価（緑）を表す．ステップには数回の評価が必要なことがある：

WorkingPrecision (1)

100桁精度演算で根を求める：

機械精度で始め，適応的に精度を100まで上げて根を求める：

アプリケーション (3)

逆関数の計算 (1)

同型写像について，その逆関数はの根である：

指数関数の近似逆関数：

これは組込みのLog関数に非常に近い：

振動周期を与える「ブラックボックス」関数：

その逆関数をプロットする：

境界値問題を解く (2)

シューティング法を使って境界値問題 , を解く：

根の両側の点を使ってカッコにいれる初期値を与える：

解をプロットする：

n 個の選点で境界値問題 , を解く：

一階の系として考える：

台形法則を使った連結に関する方程式：

初期値として0を使う：

ϵ の特定の値について解を求める：

特性と関係 (2)

方程式の多項式系の場合，NSolveはすべての解をFindRootは1つの解を求める：

FindRootは反復法を使って1つの解を求める：

NSolveは直接法を使ってすべての解を求める：

パラメータまたは厳密解を含む方程式の場合はSolve，Reduce，FindInstanceのいずれかを使う：

Solveはいくつかの解を返す：

Reduceはすべての解を列挙する：

FindInstanceは特定の例を求める：

考えられる問題 (2)

関数が複素関数の場合は，変数は複素値を持つことができる：

関数が実数のままなら，変数も実数であると考えられる：

関数を記号的に評価するのには時間がかかることがある：

関数の定義を制限して記号評価を避ける：

トップへ