Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

FindRoot

FindRoot[f,{x,x₀}]

求 f 的一个数值根，从点 x=x₀ 开始.

FindRoot[lhs==rhs,{x,x₀}]

求方程 lhs==rhs 的一个数值解.

FindRoot[{f₁,f₂,…},{{x,x₀},{y,y₀},…}]

求满足所有 f_i 的数值解.

FindRoot[{eqn₁,eqn₂,…},{{x,x₀},{y,y₀},…}]

求联立方程 eqn_i 的一个数值解.

更多信息和选项

如果变量的初始值是以列表形式给出，变量值采用相同维数的列表.
FindRoot 返回 x，y，… ，的替换列表，这和从 Solve 获得的形式相同.
FindRoot 首先局部化所有变量值，然后在变量保持符号形式的情况下计算 f，然后以数值法重复计算结果.
FindRoot 具有属性 HoldAll，实际上用 Block 局部化变量.
FindRoot[lhs==rhs,{x,x₀,x₁}] 用 x₀ 和 x₁ 作为 x 的前 2 个值进行求解，避免使用导数.
FindRoot[lhs==rhs,{x,x_start,x_min,x_max}] 搜索一个解，如果 x 超出了 x_min 到 x_max 的范围，就停止搜索.
如果用户只指定了 x 的一个初值，FindRoot 就用牛顿法求解. 如果用户指定两个初值，FindRoot 会采用割线法的变体来求解.
如果所有方程和初值都是实数，则 FindRoot 仅搜索实数根. 如果出现复数，则还要搜索复数根.
可以通过对初值加上 0.I，使 FindRoot 搜索复数根.
可以给出下列选项：

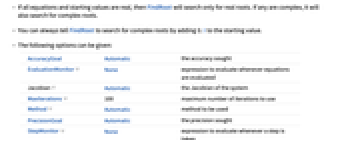
	AccuracyGoal	Automatic	搜索的准确度
	EvaluationMonitor	None	计算方程时要计算的表达式
	Jacobian	Automatic	方程组的 Jacobian
	MaxIterations	100	最大迭代次数
		Automatic	使用的方法
	PrecisionGoal	Automatic	搜索精度
	StepMonitor	None	每个步骤计算的表达式
	WorkingPrecision	MachinePrecision	内部计算的精度

AccuracyGoal 和 PrecisionGoal 的默认设置是 WorkingPrecision/2.
AccuracyGoal 的设置指定了搜索根的位置和计算函数在根处的值时要达到多少位的准确度.
PrecisionGoal 的设置指定了搜索根的位置时要采用多少位的精度.
FindRoot 会持续搜索直到实现 AccuracyGoal 或 PrecisionGoal 指定的目标中的任何一个.
如果 FindRoot 在 MaxIterations 步骤内，没有搜索到指定准确度的解，它将返回最后找到的解的近似值. 可用这个近似值为起点，再次应用 FindRoot.

范例

打开所有单元关闭所有单元

基本范例 (3)

求在附近的一个根：

求在附近的一个解：

求解一个非线性方程组：

范围 (4)

求由两个非线性方程组成的方程组的解：

求 3 变量的、由 3 个分量组成的函数的根：

可以给出一个复数初值来搜索复数根：

如果输入为实数，而函数为复变函数，则一个实数初值可能会给出一个复数结果：

推广和延伸 (1)

如果一个变量出现在初值中，则该变量被认为是向量：

选项 (9)

AccuracyGoal 和 PrecisionGoal (1)

改变误差估计的容差：

放宽计算停止的容差：

用估计的与根的相对距离作为停止计算的主要标准：

DampingFactor (1)

DampingFactor 可用来加速收敛到高阶根：

EvaluationMonitor (1)

EvaluationMonitor 可用来跟踪所用的函数计算：

Jacobian (1)

为一个“黑盒子" 函数指定 Jacobian：

如果没有指定 Jacobian，要进行额外运算来计算有限差分：

如果只知道稀疏形式，可指定稀疏模式的模板来保存计算：

检查不同方法所需的 Jacobian 计算数目：

MaxIterations (1)

限制或增大迭代次数：

缺省迭代次数是 100：

由于柔化函数在处的所有导数都为 0，停止计算：

Method (2)

方法选项在无约束条件优化中也有解释.

用不同的方法求的根：

定义一个函数，监视 FindRoot 所用的步骤和计算：

缺省（牛顿）方法：

Brent 的包围根方法需要两个初始条件来包围根：

割线法，从两个初始条件开始：

选择仿射协变牛顿法：

StepMonitor (1)

迭代步骤发生时进行监控：

在的等高线图上显示步骤：

显示步骤 (红色) 和计算 (绿色). 一个步骤可能需要几次计算：

WorkingPrecision (1)

用 100 位精度的算法求一个根：

开始时采用机器精度，然后以自适应方式将精度调整到 100 进行求解：

应用 (3)

计算反函数 (1)

对于同构的，反函数是的根：

指数函数的近似反函数：

这非常接近内置的 Log 函数：

可给出振动周期的“黑盒子”函数：

绘制它的反函数：

求边界值问题 (2)

用打靶法求解边界值问题，：

用位于根的任意一边的点给出包围初值：

绘制解：

用 n 个并置点求解边界值问题，：

将其视为一阶方程：

用梯形规则进行并置的方程：

用 0 作为初值：

ϵ 取特定值的情况下求解：

属性和关系 (2)

对一个多项式方程组，NSolve 求所有解，FindRoot 求一个解：

FindRoot 用迭代法求单个解：

NSolve 直接求出所有解：

对含有参数或有精确解的方程，用 Solve、Reduce 或 FindInstance：

Solve 将返回某些解：

Reduce 列举所有解：

FindInstance 求特定实例：

可能存在的问题 (2)

如果函数是复变函数，变量允许是复数值：

如果函数是实数函数，则变量同样取实数：

对函数进行符号式求解可能很耗时：

限制函数定义可防止符号式计算：

顶部