Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

FindVertexCover

FindVertexCover[g]

求具有最小顶点数的图 g 的顶点覆盖.

FindVertexCover[{vw,…}]

使用规则 vw 指定图 g.

更多信息

FindVertexCover 返回顶点列表.
如果没有找到顶点覆盖则 FindVertexCover 将返回一个空列表.

顶点覆盖是与每条边相关联的顶点集合.
FindVertexCover 作用于无向图、有向图、加权图、多重图和混合图.

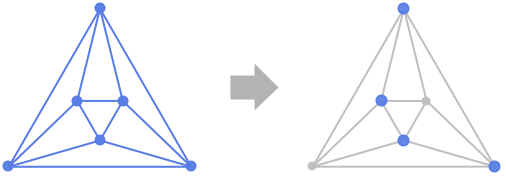
背景

FindVertexCover 求出图的单顶点覆盖，其中顶点覆盖是满足各边附带顶点条件的顶点的子集.
FindVertexCover[g] 求图 g 的最小顶点覆盖（即最小尺寸的顶点覆盖），其中 FindVertexCover[g,k] 求大小为 k 的一个顶点覆盖. 图 g 的最小顶点覆盖尺寸被称作顶点覆盖数. 求一个普通图的最小顶点覆盖中（因此也是顶点覆盖数）的问题是一个非完全多项式，这就意味着计算可能是指数式的缓慢. 然而，对于双边图而言，一个最小顶点覆盖可以在多项式时间中求出.
顶点覆盖与独立定点集（即顶点集合，其中不存在属于同一条边的两个顶点）紧密相关. 特别地，当且仅当顶点集的补集构成一个独立顶点集时该顶点集是一个顶点覆盖. 因此一个图中的顶点覆盖数和独立顶点集的数目是相同的. 此外，无向图的独立数总和（即最大独立顶点大小）和顶点覆盖数（即最小顶点覆盖大小）等于顶点数.
一个图的顶点覆盖可以通过从最大独立边集中的各边中取端点形成.（其中，独立边集是一个边的集合，其中不存在共用一个顶点的边. 最大独立边集是一个给定图可能存在的最大独立边集合.）因此，最小顶点覆盖的大小总是不大于二倍的最大独立边集大小. König–Egerváry 定理指出二分图的最大独立边集大小（即匹配数）等于其顶点覆盖数.
VertexCoverQ 可用于测试一个给定的顶点集是否能构成指定图的顶点覆盖. 因此应用 VertexCoverQ 于图顶点的任意想要求出的子集就是求多个顶点覆盖的一种显而易见的方法. 类似地， FindIndependentVertexSet 可用于在图中求出一个或多个最大独立顶点集，而其补集即为顶点覆盖. FindEdgeCover 执行的是与 FindVertexCover 对图的边覆盖相类似的测试.

范例

打开所有单元关闭所有单元

基本范例 (1)

求顶点覆盖：

显示覆盖：

范围 (7)

FindVertexCover 适用于无向图：

有向图：

加权图：

多重图：

混合图：

使用规则指定图：

FindVertexCover 可用于大规模图：

属性和关系 (6)

FindVertexCover 的结果可以用 VertexCoverQ 检验：

当一组顶点集的补集是独立集时，该顶点集为一个顶点覆盖：

检验顶点集的补集是独立的：

顶点覆盖和最大独立集的总大小等于顶点数：

GraphComplement 中的顶点覆盖的补集是原图中的一个团：

使用相同的嵌入方法，计算补集：

它的补集是一个团：

完全二分图含有大小为的顶点覆盖：

二分图中的最大独立边集具有和最小顶点覆盖相同的大小：

顶部