FiniteFieldIndex

FiniteFieldIndex[u]

gives the index of the FiniteFieldElement object u.

Details

  • FiniteFieldIndex has the Listable attribute.
  • FiniteFieldIndex[u] is equivalent to u["Index"].
  • If u is an element of FiniteField[p,f,"Polynomial"], then 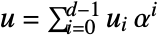, where α is the field generator and d is the degree of f. The index ind of u satisfies IntegerDigits[ind,p,d]=={ud-1,…,u0}.
  • If u is a nonzero element of FiniteField[p,f,"Exponential"], then 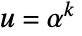, with 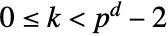, where α is the field generator and d is the degree of f. The index ind of u satisfies ind==k+1. The index of the field zero is 0.

Examples

open allclose all

Basic Examples  (1)

Create a matrix of finite field elements:

Find the indices of matrix elements:

Scope  (3)

Find the index of a finite field element:

Use a finite field in the exponential representation:

Find indices of a vector and a matrix of finite field elements:

Properties & Relations  (3)

For a single field element, FiniteFieldIndex[u] is equivalent to u["Index"]:

FiniteFieldIndex can be applied to lists of elements:

Use FromFiniteFieldIndex to get field elements with specified indices:

Convert elements of a finite field to polynomials in a variable representing the field generator:

Wolfram Research (2024), FiniteFieldIndex, Wolfram Language function, https://reference.wolfram.com/language/ref/FiniteFieldIndex.html.

Text

Wolfram Research (2024), FiniteFieldIndex, Wolfram Language function, https://reference.wolfram.com/language/ref/FiniteFieldIndex.html.

CMS

Wolfram Language. 2024. "FiniteFieldIndex." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FiniteFieldIndex.html.

APA

Wolfram Language. (2024). FiniteFieldIndex. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FiniteFieldIndex.html

BibTeX

@misc{reference.wolfram_2025_finitefieldindex, author="Wolfram Research", title="{FiniteFieldIndex}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FiniteFieldIndex.html}", note=[Accessed: 22-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_finitefieldindex, organization={Wolfram Research}, title={FiniteFieldIndex}, year={2024}, url={https://reference.wolfram.com/language/ref/FiniteFieldIndex.html}, note=[Accessed: 22-February-2025 ]}