FromFiniteField[a,ff]
converts the element a of the prime subfield of the finite field ff to an integer.
FromFiniteField[expr,ff,t]
converts the elements of the finite field ff in the coefficients of the rational expression expr to polynomials in t, where t represents the field generator.


FromFiniteField
FromFiniteField[a,ff]
converts the element a of the prime subfield of the finite field ff to an integer.
FromFiniteField[expr,ff,t]
converts the elements of the finite field ff in the coefficients of the rational expression expr to polynomials in t, where t represents the field generator.
Details
- FromFiniteField replaces elements
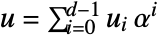 of ff, where α=ff[{0,1}] is the field generator, with polynomials
of ff, where α=ff[{0,1}] is the field generator, with polynomials 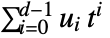 .
. - FromFiniteField goes inside List, Plus, Times and integer Power in expr.
Examples
open all close allBasic Examples (4)
Convert an element of the prime subfield of a finite field to an integer:
Convert an element of a finite field to a polynomial in a variable representing the field generator:
Convert prime field coefficients in a rational expression to integers:
Convert finite field coefficients in a rational expression to polynomials in the field generator:
Scope (3)
Convert an element of the prime subfield of a finite field to an integer:
b is not an element of the prime subfield:
Convert an element of a finite field to a polynomial in a variable representing the field generator:
Convert finite field coefficients in a rational expression to polynomials in the field generator:
Properties & Relations (2)
ToFiniteField converts coefficients to finite field elements, with t representing the field generator:
FiniteFieldIndex gives indices of field elements:
FromFiniteField gives integers only for elements of the prime subfield:
Related Guides
History
Text
Wolfram Research (2024), FromFiniteField, Wolfram Language function, https://reference.wolfram.com/language/ref/FromFiniteField.html.
CMS
Wolfram Language. 2024. "FromFiniteField." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FromFiniteField.html.
APA
Wolfram Language. (2024). FromFiniteField. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FromFiniteField.html
BibTeX
@misc{reference.wolfram_2025_fromfinitefield, author="Wolfram Research", title="{FromFiniteField}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FromFiniteField.html}", note=[Accessed: 01-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_fromfinitefield, organization={Wolfram Research}, title={FromFiniteField}, year={2024}, url={https://reference.wolfram.com/language/ref/FromFiniteField.html}, note=[Accessed: 01-January-2026]}