FiniteGroupData[name,"property"]
给出 name 指定的有限群的指定属性值.
FiniteGroupData["class"]
给出指定类的有限群的列表.


FiniteGroupData
FiniteGroupData[name,"property"]
给出 name 指定的有限群的指定属性值.
FiniteGroupData["class"]
给出指定类的有限群的列表.
更多信息












- 群可以通过诸如 "C3","Quaternion" 和 {"SymmetricGroup",4} 的名称指定.
- FiniteGroupData[name] 给出 name 指定群的名称的标准形式.
- FiniteGroupData[patt] 给出匹配字符串模式 patt 的所有群名称的列表.
- FiniteGroupData[] 和 FiniteGroupData[All] 给出可用的已命名有限群,如 "Quaternion",和无限族的小成员——如 {"SymmetricGroup",deg} 的前 10 个成员——的列表. FiniteGroupData 可以与这些无限族的其他成员一起使用.
- FiniteGroupData[{n, id},…] 给出标识符 id 的 n 阶有限群的数据.
- FiniteGroupData[n] 给出阶数为 n 的非同构有限群列表.
- FiniteGroupData[;;n] 给出阶数最多 n 的阶数的非同构列表.
- FiniteGroupData[n1;;n2] 给出从 n1 到 n2 阶的非同构群的列表.
- FiniteGroupData[{"type", id}, …] 给出标识符 id 的特定类有限群的数据. 标识符通常是一个整数或一个整数列表.
- 群的基本族群包括:
-
{"AlternatingGroup",n} 交错群 
{"CrystallographicPointGroup",n} 晶体群 (三维晶体学点群, 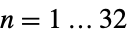
{"CyclicGroup",n} 循环群 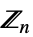
{"CyclicGroupUnits",n} 循环群的单位群 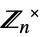
{"DicyclicGroup",n} 双循环群 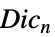
{"DihedralGroup",n} 二面体群 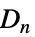
{"PointGroup",id} 三维点群 {"SymmetricGroup",n} 对称群 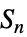
- 有限单群包括:
-
{"ProjectiveSpecialLinearGroup",{n,q}} 特殊射影线性群 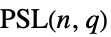
{"ProjectiveSymplecticGroup",{n,q}} 射影辛群 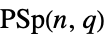
{"ChevalleyGroupB",{n,q}} 特殊 Chevalley 群 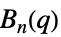
{"ChevalleyGroupD",{n,q}} 特殊 Chevalley 群 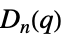
{"ChevalleyGroupE",{n,q}} 例外 Chevalley 群 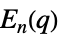 ,
, 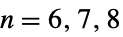
{"ChevalleyGroupF",{4,q}} 例外 Chevalley 群 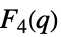
{"ChevalleyGroupG",{2,q}} 例外 Chevalley 群 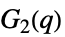
{"ReeGroupF",q} Ree 群 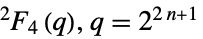
{"ReeGroupG",q} Ree 群 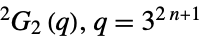
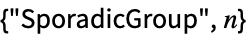
散在单群, 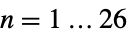
{"SteinbergGroupA",{n,q}} Steinberg 酉群 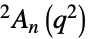
{"SteinbergGroupD",{n,q}} Steinberg 正交群 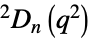
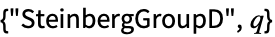
Steinberg 正交群 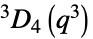
{"SteinbergGroupE",q} Steinberg 正交群 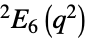

Suzuki 群 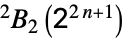
- 特殊群的指定包括:
-
{"AbelianGroup",{m,n,…}} 阿贝尔群 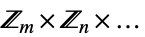
{"DirectProduct",{group1,group2,…}} 群的直积 {"SemidirectProduct",{group1,group2}} 群的半直积(半直积 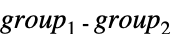 ,其中
,其中 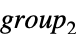 在结果中是正常的)
在结果中是正常的) - FiniteGroupData["Properties"] 给出群所具有的属性列表.
- 基本群属性包括:
-
"Center" 群的中心(换位元素子群) "CenterElements" 中心子群的元素 "ClassNumber" 类的数目 "CommutatorSubgroup" 交换子子群 "CommutatorSubgroupElements" 换位子群的元素 "ConjugacyClasses" 共轭类 "ElementNames" 元素名称列表 "Elements" 群的元素 "Exponent" 群的指数 "Generators" 生成元元素 "InverseGenerators" 生成元元素的逆 "Inverses" 逆元素 "MultiplicationTable" 乘法表 "NormalSubgroupElements" 正规子群的元素 "NormalSubgroups" 正规子群 "Order" 全部元素数量 "SubgroupElements" 子群的元素 "Subgroups" 子群 "SylowSubgroupCounts" Sylow 子群的大小 "SylowSubgroupElements" Sylow 子群的元素 "SylowSubgroups" 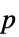 -Sylow 子群
-Sylow 子群 - 一个群的元素用从 1 到群阶的整数来指定,其中 1 对应单位元素.
- 群结构属性包括:
-
"AutomorphismGroup" 自同构群 "InnerAutomorphismGroup" 内自同构群 "IsomorphicGroups" 同构群列表 "OuterAutomorphismGroup" 外自同构群 "QuotientGroups" 商群列表 "SchurMultiplier" 舒尔乘子 - 置换群属性包括:
-
"CycleIndex" 轮换指标 "Cycles" 轮换 "PermutationRepresentation" 置换表示 "PermutationGroupRepresentation" 表示为 Wolfram 语言置换群 "Transitivity" 传递性水平 - 其它属性包括:
-
"DefiningRelations" 描述群代数的关系 "CayleyGraph" 选择的内置生成器的 Cayley 图 "Classes" 群所属的类 "CycleGraph" 环图 "Information" 关于群的信息 "ParameterRange" 对参数的假设 - 群表示属性包括:
-
"CharacterTable" 群元素特征 "ConjugacyClassNames" 共轭类的名称 "ConjugacyClassSizes" 共轭类的大小 "MatrixRepresentation" 矩阵表示 "RepresentationDimensions" 表示的维数 "RepresentationNames" 表示的名称 "SpaceRepresentation" 表示为三维笛卡尔坐标变换 - 结晶点群的其它属性包括:
-
"BravaisLattices" 相容的 Bravais 晶格 "CrystalForm" 晶体形式 "CrystalSystem" 晶体系统 "HermannMauguin" Hermann–Mauguin 符号 "Orbifold" 迹形符号 "PointGroupType" 点群类型 "Schoenflies" Schoenflies 符号 "Shubnikov" Shubnikov 符号 - FiniteGroupData["Classes"] 给出所有支持的类型的列表.
- FiniteGroupData[name,"Classes"] 给出特定的群所属的所有类型的列表.
- FiniteGroupData[name,"class"] 根据一个对应于 name 的群是否属于指定的类型,给出 True 或 False.
- FiniteGroupData["class"] 给出 FiniteGroupData[] 中属于特定类型的有限群列表.
- FiniteGroupData["class",n] 给出指定类型中 n 阶有限群的一个列表.
- FiniteGroupData["class",;;n] 给出指定类型中阶数小于或等于 n 的有限群列表.
- FiniteGroupData["class",n;;] 给出指定类型中阶数大于或等于 n 的所有标准有限群列表.
- FiniteGroupData["class",n1;;n2] 给出指定类型中阶数大于 n1 且小于 n2 的所有标准有限群列表.
- 群的类型包括:
-
"Abelian" 阿贝尔群 "Alternating" 交错群 "Cyclic" 循环群 "Dihedral" 二面体群 "Perfect" 完美群 "Simple" 简单群 "Solvable" 可解群 "Sporadic" 散在群 "Symmetric" 对称群 "Transitive" 可迁群 - 群的否定类包括:
-
"Nonabelian" 非阿贝尔群 "Nonalternating" 非交错群 "Noncyclic" 非循环群 "Nondihedral" 非二面体群 "Nonperfect" 非完美群 "Nonsimple" 非简单群 "Nonsolvable" 不可解群 "Nonsporadic" 非散在群 "Nonsymmetric" 非对称群 "Nontransitive" 非可迁群 - 如果一个群与同阶的交错群、循环群、二面体群或对称群同构,则该群属于 "Alternating"、"Cyclic"、"Dihedral" 或 "Symmetric" 类.
- 如果相应的置换表示是可迁的,则该群属于 "Transitive" 类. {"DirectProduct",{group1,group2,…}} 的置换表示是在商群的各个作用域的不相交并集上构建的,因此不是可迁的.
- 与命名相关的属性包括:
-
"AlternateNames" 其它的英文名称,为字符串 "AlternateStandardNames" 其它的标准 Wolfram 语言名称 "Name" 英文名称,为字符串 "Notation" 群的标记 "ShortName" 简称,为字符串 "StandardName" 标准 Wolfram 语言名称 - FiniteGroupData[name,"Information"] 给出一个超链接,指向指定群的更多信息.
- 用 FiniteGroupData 可能需要网络连接.
范例
打开所有单元 关闭所有单元范围 (34)
名称和类型 (6)
所有已命名的有限群和无限族的小成员列表,其中多数是互相同构的:
FiniteGroupData[] 中属于给定类别的群列表:
FiniteGroupData[n] 返回阶数为 n 的非同构群列表,第一个具有阿贝尔群,其它是非阿贝尔群:
当 FiniteGroupData 不具有给定群的已命名版本,它被指定为 {order,index}:
属性值 (3)
详细属性 (21)
名称和记号 (3)
基本群属性 (4)
群表示 (4)
群结构 (8)
推广和延伸 (2)
但是,大多数属性要求这些参数的值为整数. 在这样的情况下,返回 Missing["NotApplicable"]:
属性和关系 (3)
FiniteGroupCount[n] 给出 n 阶有限群的数量:
一致地,当同构阶数说明时,FiniteGroupData 返回非同构群列表:
FiniteAbelianGroupCount[n] 给出 n 阶阿贝尔群的数量:
整数模 n 的环(ring)的单元组成的群总是阿贝尔群,但不总是循环的:
如果存在元素的阶数是群阶数,则该群是循环的. {"CyclicGroupUnits", n} 的阶数是 EulerPhi[n],而 CarmichaelLambda[n] 给出元素之间的最大阶数.
在质数 p≠2 并且 k≥1 的情况下,条件 EulerPhi[n]CarmichaelLambda[n] 只对形式为 2、4、pk、2pk 的正整数 n 才成立.
可能存在的问题 (1)
文本
Wolfram Research (2008),FiniteGroupData,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FiniteGroupData.html (更新于 2020 年).
CMS
Wolfram 语言. 2008. "FiniteGroupData." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/FiniteGroupData.html.
APA
Wolfram 语言. (2008). FiniteGroupData. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FiniteGroupData.html 年
BibTeX
@misc{reference.wolfram_2025_finitegroupdata, author="Wolfram Research", title="{FiniteGroupData}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FiniteGroupData.html}", note=[Accessed: 18-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_finitegroupdata, organization={Wolfram Research}, title={FiniteGroupData}, year={2020}, url={https://reference.wolfram.com/language/ref/FiniteGroupData.html}, note=[Accessed: 18-February-2026]}