FisherRatioTest

FisherRatioTest[data]

data の分散が1かどうかの検定を行う．

FisherRatioTest[{data1,data2}]

data1 と data2の分散が等しいかどうかの検定を行う．

FisherRatioTest[dspec,]

について分散尺度を調べる．

FisherRatioTest[dspec,,"property"]

"property"の値を返す．

詳細とオプション

  • FisherRatioTestは，帰無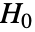仮説 と対立仮説 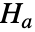で検定を行う．
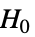
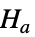
  • data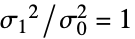
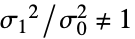
    {data1,data2}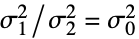
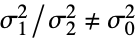
  • ただし，σi2 は dataiの母分散である．
  • デフォルトで，確率値つまり 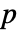値が返される．
  • 小さい 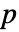値は 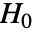が真である可能性が低いことを示す．
  • dspec 中の data は一変量{x1,x2,…}でなければならない．
  • 引数 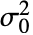は任意の実数でよい．
  • FisherRatioTestでは，データは正規分布に従っていなければならない．
  • FisherRatioTest[data,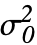,"HypothesisTestData"]はHypothesisTestDataオブジェクト htd を返す．これは htd["property"]として追加的な検定結果と特性の抽出に使うことができる．
  • FisherRatioTest[data,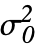,"property"]を使って直接"property"の値を与えることができる．
  • 検定結果のレポートに関連する特性
  • "DegreesOfFreedom"検定で使用する自由度
    "PValue" 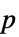値のリスト
    "PValueTable" 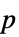値のフォーマットされた表
    "ShortTestConclusion"検定結果の簡単な説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計と 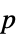値のペアのリスト
    "TestDataTable" 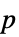値と検定統計のフォーマットされた表
    "TestStatistic"検定統計のリスト
    "TestStatisticTable"検定統計のフォーマットされた表
  • サイズ 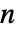のサンプルが1つだけ与えられた場合，検定統計は 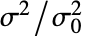に基づき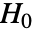，の下でChiSquareDistribution[n-1]に従うと仮定される．
  • サイズ 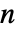と 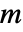の2つのサンプルが与えられた場合，検定統計は 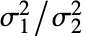に基づき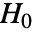，の下でFRatioDistribution[n-1,m-1]に従うとa仮定される．
  • FisherRatioTestは分散が等しい場合はしばしばF検定と呼ばれる．
  • 使用可能なオプション
  • AlternativeHypothesis "Unequal"対立仮説のための不等式
    SignificanceLevel 0.05診断とレポートのための切捨て
    VerifyTestAssumptions Automaticどの診断検定を実行するかを設定する
  • FisherRatioTestでは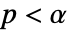， のときにのみ 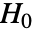が棄却されるような切捨て 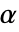が選ばれる．"TestConclusion"および"ShortTestConclusion"特性に使われる 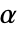の値はSignificanceLevelオプションで制御される．値 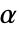は正規性と対称性の検定を含む仮定の診断検定にも使われる．デフォルトで 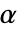は0.05に設定される．
  • FisherRatioTestのVerifyTestAssumptionsの名前付き設定
  • "Normality"すべてのデータが正規分布に従うことを検証する

例題

すべて開くすべて閉じる

例  (2)

2つの母分散を等価性について調べる：

さらに特性を抽出するためにHypothesisTestDataオブジェクトを作る：

調べる特性：

母分散を特定の値と比べる：

対立仮説 について検定を行う：

スコープ  (9)

検定  (7)

母分散が1であるかどうかを検定する：

においては， 値は通常大きい：

が偽である場合は， 値は通常小さい：

母分散と特定の値を比べる：

2つの母分散を比べる：

分散が等しい場合は， 値は通常大きい：

分散が等しくない場合は， 値は通常小さい：

2つのデータ集合の分散比が特定の値であるかどうかを検定する：

以下の形式は等しい：

を決定する場合には，データ集合の順序を考慮すべきである：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

抽出に使用できる特性：

HypothesisTestDataオブジェクトから特性をいくつか抽出する：

値，検定統計，および自由度：

任意数の特性を同時に抽出する：

値，検定統計，および自由度：

レポート  (2)

検定結果を表にする：

表の値は，"TestData"を使って抽出できる：

値あるいは検定統計を表にする：

表からの 値：

表からの検定統計：

オプション  (8)

AlternativeHypothesis  (3)

デフォルトで両側検定が行われる：

対 を検定する：

両側検定を行う．あるいは片側検定を代りに行う：

対 を検定する：

対 を検定する：

対 を検定する：

ヌル値が与えられている場合に，片側検定を代りに行う：

対 を検定する：

対 を検定する：

SignificanceLevel  (2)

診断検定の有意水準を設定する：

デフォルトで0.05が使われる：

有意水準は"TestConclusion"と"ShortTestConclusion"にも使われる：

VerifyTestAssumptions  (3)

診断は，AllあるいはNoneを使ってまとめて制御することができる：

すべての仮定を検証する：

どの仮定もチェックしない：

診断は個々に制御することができる：

正規性をチェックする：

正規性の仮定をTrueに設定する：

シミュレーションを行う場合は，診断検定を行わないようにすると有益であることが多い：

検定の仮定は意図的に有効になっているので，時間が大幅に短縮できる：

結果は全く同じである：

アプリケーション  (1)

ある研究室が電圧計をより正確であると言われているものに替えることを考慮している．新しい電圧計の製造業者は，電圧計の効率性を判断するために検定を行うことを許可している．検査技師が9ボルトに設定された15個のパワーサプライで生成される電圧を測定した：

PairedTTestは，2つの電圧計からの数値はあまり変わらないことを示す：

等分散の検定は，新しい電圧計が古いものよりもエラーが少ないことを示す：

特性と関係  (8)

1つのデータ集合が与えられた場合，フィッシャー(Fisher)の比率検定はLeveneTestに等しい：

1つのデータ集合についてBrownForsytheTestにも等しい：

長さ の1つのデータ集合が与えられた場合，検定統計は においてChiSquareDistribution[n-1]に従う：

自由度の最尤推定値は に近い：

2つのサンプルが与えられた場合のFisherRatioTestの検定統計：

長さが と である2つのデータ集合が与えられた場合，検定統計は においてFRatioDistribution[n-1,m-1]に従う：

フィッシャーの比率検定は，正規性の仮定を感知する度合が非常に高い：

検定統計の分布はChiSquareDistribution[n-1]ではない：

NormalDistribution[μ,σ]のサイズが でサンプル分散が であるサンプルにおいては，確率変数はChiSquareDistribution[n-1]に従う：

以下はFRatioDistribution[n-1,m-1]に従う：

FisherRatioTestの検定統計は，FRatioDistribution[n-1,m-1]に従う：

フィッシャーの比率検定は，入力がTimeSeriesのときにのみ値に使うことができる：

フィッシャーの比率検定は，入力がTemporalDataのときはすべての値に使うことができる：

すべての値のみを検定する：

2つの経路の分散が等しいかどうかの検定を行う：

考えられる問題  (1)

フィッシャーの比率検定は，正規分布に従うデータにのみ使える：

データが正規分布に従わない場合は，ConoverTestあるいはSiegelTukeyTestを使う：

おもしろい例題  (1)

帰無仮説 が真であるときの統計量を計算する：

特定の対立仮説による検定統計：

検定統計の分布を比較する：

Wolfram Research (2010), FisherRatioTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/FisherRatioTest.html.

テキスト

Wolfram Research (2010), FisherRatioTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/FisherRatioTest.html.

CMS

Wolfram Language. 2010. "FisherRatioTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FisherRatioTest.html.

APA

Wolfram Language. (2010). FisherRatioTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FisherRatioTest.html

BibTeX

@misc{reference.wolfram_2024_fisherratiotest, author="Wolfram Research", title="{FisherRatioTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/FisherRatioTest.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fisherratiotest, organization={Wolfram Research}, title={FisherRatioTest}, year={2010}, url={https://reference.wolfram.com/language/ref/FisherRatioTest.html}, note=[Accessed: 22-November-2024 ]}