WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

FourierDCT
✖
FourierDCT

✖
FourierDCT[list]

finds the Fourier discrete cosine transform of a list of real numbers.

✖
FourierDCT[list,m]

finds the Fourier discrete cosine transform of type m.

Details

  • Possible types m of discrete cosine transform for a list 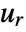of length 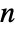giving a result 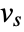are:
  • 1 (DCT-I)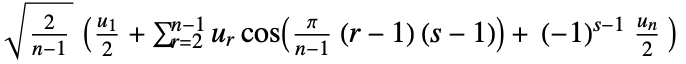
    2 (DCT-II)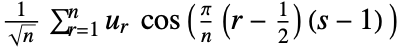
    3 (DCT-III)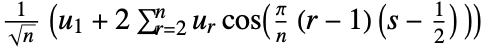
    4 (DCT-IV)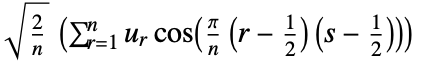
  • FourierDCT[list] is equivalent to FourierDCT[list,2].
  • The inverse discrete cosine transforms for types 1, 2, 3, and 4 are types 1, 3, 2, and 4, respectively.
  • The list given in FourierDCT[list] can be nested to represent an array of data in any number of dimensions.
  • The array of data must be rectangular.
  • If the elements of list are exact numbers, FourierDCT begins by applying N to them.
  • FourierDCT can be used on SparseArray objects.

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

Find a discrete cosine transform:

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-cp3avz
Out[1]=1

Find the inverse discrete cosine transform:

In[2]:=2
✖
https://wolfram.com/xid/0d6fi5pnaz-or46i9
Out[2]=2

Find a discrete cosine transform of type 1 (DCT-I):

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-c3pfpi
Out[1]=1

Find the inverse discrete cosine transform:

In[2]:=2
✖
https://wolfram.com/xid/0d6fi5pnaz-gcl549
Out[2]=2

Scope  (2)Survey of the scope of standard use cases

Use machine arithmetic to compute the discrete cosine transform:

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-ey73mv
In[2]:=2
✖
https://wolfram.com/xid/0d6fi5pnaz-cwvgdf
Out[2]=2

Use 24-digit precision arithmetic:

In[3]:=3
✖
https://wolfram.com/xid/0d6fi5pnaz-fyo9i6
Out[3]=3

A two-dimensional discrete cosine transform:

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-bbgp1y
In[2]:=2
✖
https://wolfram.com/xid/0d6fi5pnaz-bmat6k
Out[2]=2

A five-dimensional discrete cosine transform:

In[3]:=3
✖
https://wolfram.com/xid/0d6fi5pnaz-b6uq7
In[4]:=4
✖
https://wolfram.com/xid/0d6fi5pnaz-3gt9n
Out[4]=4

Generalizations & Extensions  (2)Generalized and extended use cases

The list may have complex values:

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-c6gm36
Out[1]=1

You can use "I", "II", "III", or "IV" for the types 1, 2, 3, and 4, respectively:

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-dbvmy9
Out[1]=1

Applications  (3)Sample problems that can be solved with this function

Compressing Image Data  (1)

Import some image data:

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-eucewz
Out[1]=1

The two-dimensional DCT:

In[2]:=2
✖
https://wolfram.com/xid/0d6fi5pnaz-fhhdzo

The diagonal spectra shows exponential decay:

In[3]:=3
✖
https://wolfram.com/xid/0d6fi5pnaz-kpcgtm
Out[3]=3

Truncate modes in each axis, effectively compressing by a factor of :

In[4]:=4
✖
https://wolfram.com/xid/0d6fi5pnaz-mf75zk

Invert the DCT:

In[5]:=5
✖
https://wolfram.com/xid/0d6fi5pnaz-bh9ss5
Out[5]=5

Cosine Series Expansion  (1)

Get an expansion for an even function as a sum of cosines:

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-e4it3w

The function values on a uniformly spaced grid with points on :

In[2]:=2
✖
https://wolfram.com/xid/0d6fi5pnaz-cxv768
Out[2]=2

Compute the DCT-III and renormalize:

In[3]:=3
✖
https://wolfram.com/xid/0d6fi5pnaz-904ye

The function has, in effect, been periodized with a particular symmetry:

In[4]:=4
✖
https://wolfram.com/xid/0d6fi5pnaz-b84knh
Out[4]=4

Plot the expansion error where the points are defined:

In[5]:=5
✖
https://wolfram.com/xid/0d6fi5pnaz-tkscl
Out[5]=5

Chebyshev Basis Expansion  (1)

Get an expansion for a function in the Chebyshev polynomials:

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-fcuwgs

The values of the function at the Chebyshev nodes:

In[2]:=2
✖
https://wolfram.com/xid/0d6fi5pnaz-6uyoe
Out[2]=2

Find the Chebyshev coefficients:

In[3]:=3
✖
https://wolfram.com/xid/0d6fi5pnaz-xnku2

Show the error:

In[4]:=4
✖
https://wolfram.com/xid/0d6fi5pnaz-gq2wl0
Out[4]=4

Properties & Relations  (3)Properties of the function, and connections to other functions

DCT-I and DCT-IV are their own inverses:

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-ewwesq
In[2]:=2
✖
https://wolfram.com/xid/0d6fi5pnaz-ewncg2
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0d6fi5pnaz-qxzky
Out[3]=3

DCT-II and DCT-III are inverses of each other:

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-f5nepf
In[2]:=2
✖
https://wolfram.com/xid/0d6fi5pnaz-lidfoy
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0d6fi5pnaz-chdoia
Out[3]=3

The DCT is equivalent to matrix multiplication:

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-1m6g0
In[2]:=2
✖
https://wolfram.com/xid/0d6fi5pnaz-ehhafb
In[3]:=3
✖
https://wolfram.com/xid/0d6fi5pnaz-bgwh89
In[4]:=4
✖
https://wolfram.com/xid/0d6fi5pnaz-b1d7lk
Out[4]=4

Possible Issues  (1)Common pitfalls and unexpected behavior

FourierDCT always returns normalized results:

In[1]:=1
✖
https://wolfram.com/xid/0d6fi5pnaz-pzjmzy

To get unnormalized results, you can multiply by the normalization:

In[2]:=2
✖
https://wolfram.com/xid/0d6fi5pnaz-bj7byi
In[3]:=3
✖
https://wolfram.com/xid/0d6fi5pnaz-gpknim
In[4]:=4
✖
https://wolfram.com/xid/0d6fi5pnaz-jnv8nc
Wolfram Research (2007), FourierDCT, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierDCT.html.
✖
Wolfram Research (2007), FourierDCT, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierDCT.html.

Text

Wolfram Research (2007), FourierDCT, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierDCT.html.

✖
Wolfram Research (2007), FourierDCT, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierDCT.html.

CMS

Wolfram Language. 2007. "FourierDCT." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FourierDCT.html.

✖
Wolfram Language. 2007. "FourierDCT." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FourierDCT.html.

APA

Wolfram Language. (2007). FourierDCT. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierDCT.html

✖
Wolfram Language. (2007). FourierDCT. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierDCT.html

BibTeX

@misc{reference.wolfram_2025_fourierdct, author="Wolfram Research", title="{FourierDCT}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/FourierDCT.html}", note=[Accessed: 02-June-2025 ]}

✖
@misc{reference.wolfram_2025_fourierdct, author="Wolfram Research", title="{FourierDCT}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/FourierDCT.html}", note=[Accessed: 02-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_fourierdct, organization={Wolfram Research}, title={FourierDCT}, year={2007}, url={https://reference.wolfram.com/language/ref/FourierDCT.html}, note=[Accessed: 02-June-2025 ]}

✖
@online{reference.wolfram_2025_fourierdct, organization={Wolfram Research}, title={FourierDCT}, year={2007}, url={https://reference.wolfram.com/language/ref/FourierDCT.html}, note=[Accessed: 02-June-2025 ]}