FourierCosTransform[f[t],t,ω]
gives the symbolic Fourier cosine transform of f[t] in the variable t as F[ω] in the variable ω.
FourierCosTransform[f[t],t,![]() ]
]
gives the numeric Fourier cosine transform at the numerical value ![]() .
.
FourierCosTransform[f[t1,…,tn],{t1,…,tn},{ω1,…,ωn}]
gives the multidimensional Fourier cosine transform of f[t1,…,tn].




FourierCosTransform
FourierCosTransform[f[t],t,ω]
gives the symbolic Fourier cosine transform of f[t] in the variable t as F[ω] in the variable ω.
FourierCosTransform[f[t],t,![]() ]
]
gives the numeric Fourier cosine transform at the numerical value ![]() .
.
FourierCosTransform[f[t1,…,tn],{t1,…,tn},{ω1,…,ωn}]
gives the multidimensional Fourier cosine transform of f[t1,…,tn].
Details and Options



- The Fourier cosine transform is a particular way of viewing the Fourier transform without the need for complex numbers or negative frequencies.
- Joseph Fourier designed his famous transform using this and the Fourier sine transform, and they are still used in applications like signal processing, statistics and image and video compression.
- The Fourier cosine transform of the time domain function
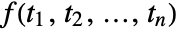 is the frequency domain function
is the frequency domain function 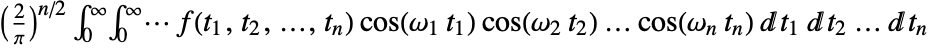 for
for  :
: - The Fourier cosine transform of a function
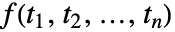 is by default defined to be
is by default defined to be 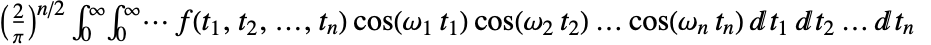 .
. - The multidimensional Fourier cosine transform of a function
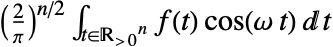 is by default defined to be
is by default defined to be  or when using vector notation,
or when using vector notation, ![(2/pi)^(n/2)int_(t in TemplateBox[{}, PositiveReals]^n) f(t) cos(omega t)dt (2/pi)^(n/2)int_(t in TemplateBox[{}, PositiveReals]^n) f(t) cos(omega t)dt](Files/FourierCosTransform.en/11.png) .
. - Different choices of definitions can be specified using the option FourierParameters.
- The integral is computed using numerical methods if the third argument,
 , is given a numerical value.
, is given a numerical value. - The asymptotic Fourier cosine transform can be computed using Asymptotic.
- There are several related Fourier transformations:
-
FourierTransform infinite continuous-time functions (FT) FourierSequenceTransform infinite discrete-time functions (DTFT) FourierCoefficient finite continuous-time functions (FS) Fourier finite discrete-time functions (DFT) - The Fourier cosine transform is an automorphism in the Schwartz vector space of functions whose derivatives are rapidly decreasing and thus induces an automorphism in its dual: the space of tempered distributions. These include absolutely integrable functions, well-behaved functions of polynomial growth and compactly supported distributions.
- Hence, FourierCosTransform not only works with absolutely integrable functions on
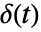 , but it can also handle a variety of tempered distributions such as DiracDelta to enlarge the pool of functions or generalized functions it can effectively transform.
, but it can also handle a variety of tempered distributions such as DiracDelta to enlarge the pool of functions or generalized functions it can effectively transform. - The lower limit of the integral is effectively taken to be
![TemplateBox[{0, -}, Superscript] TemplateBox[{0, -}, Superscript]](Files/FourierCosTransform.en/14.png) , so that the Fourier cosine transform of the Dirac delta function
, so that the Fourier cosine transform of the Dirac delta function 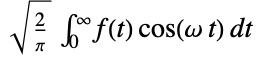 is equal to
is equal to 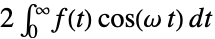 . »
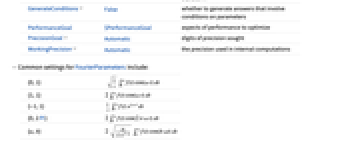
. » - The following options can be given:
-
AccuracyGoal Automatic digits of absolute accuracy sought Assumptions $Assumptions assumptions to make about parameters FourierParameters {0,1} parameters to define the Fourier cosine transform GenerateConditions False whether to generate answers that involve conditions on parameters PerformanceGoal $PerformanceGoal aspects of performance to optimize PrecisionGoal Automatic digits of precision sought WorkingPrecision Automatic the precision used in internal computations - Common settings for FourierParameters include:
-
{0,1} 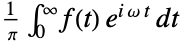
{1,1} 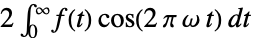
{-1,1} 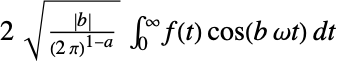
{0,2Pi} 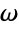
{a,b} 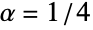
Examples
open all close allBasic Examples (6)
Compute the Fourier cosine transform of a function:
Plot the function and its Fourier cosine transform:
Fourier cosine transform of reciprocal square root:
For a different convention, change the parameters:
Fourier cosine transform of a Gaussian is another Gaussian:
Compute the Fourier cosine transform of a multivariate function:
Scope (39)
Basic Uses (3)
Algebraic Functions (4)
Exponential and Logarithmic Functions (3)
Trigonometric Functions (5)
Special Functions (7)
Sinc function:
Fourier cosine transforms of expressions involving ExpIntegralEi:
Expression involving Erfc:
Expression involving SinIntegral:
Cosine transforms for BesselJ functions:
Cosine transforms for BesselY functions:
Piecewise Functions and Distributions (4)
Fourier cosine transform of a piecewise function:
Restriction of a sine function to a half-period:
Transforms in terms of FresnelC:
Periodic Functions (2)
Generalized Functions (4)
Fourier cosine transforms of expressions involving HeavisideTheta:
Fourier cosine transforms involving DiracDelta:
Fourier cosine transform involving HeavisideLambda:
Fourier cosine transform involving HeavisidePi:
Multivariate Functions (2)
Fourier cosine transforms of exponentials in two variables:
Fourier cosine transform of product of exponential and SquareWave:
Formal Properties (3)
Options (8)
AccuracyGoal (1)
The option AccuracyGoal sets the number of digits of accuracy:
Assumptions (1)
Fourier cosine transform of BesselJ is a piecewise function:
FourierParameters (3)
Fourier cosine transform for the unit box function with different parameters:
Create a nicely formatted table of the results:
Use a nondefault setting for a different definition of transform:
To get the inverse, use the same FourierParameters setting:
Set up your particular global choice of parameters once per session:
GenerateConditions (1)
Use GenerateConditionsTrue to get parameter conditions for when a result is valid:
PrecisionGoal (1)
The option PrecisionGoal sets the relative tolerance in the integration:
WorkingPrecision (1)
If a WorkingPrecision is specified, the computation is done at that working precision:
Applications (4)
Ordinary Differential Equations (1)
Consider the following ODE with initial condition ![]() :
:
Apply the Fourier cosine transform to the ODE:
Solve for the Fourier cosine transform of ![]() :
:
Find the inverse Fourier cosine transform with ![]() and
and ![]() :
:
Compare with DSolveValue:
Partial Differential Equations (1)
Solve the heat equation for ![]() ,
, ![]() :
: ![]() with initial condition
with initial condition ![]() for
for ![]() and Neumann boundary condition
and Neumann boundary condition ![]() for
for ![]() .
.
Apply the Fourier cosine transform to the ODE on ![]() :
:
Compute the inverse cosine transform of the exponential functions:
The convolution property gives the inverse cosine transform of the first summand to get the solution:
Consider the special case with ![]() ,
, ![]() and
and ![]() :
:
Compare with DSolveValue:
Plot the initial conditions and solutions for different values of ![]() .
.
Evaluation of Integrals (2)
Properties & Relations (4)
By default, the Fourier cosine transform of ![]() is:
is:
For ![]() , the definite integral becomes:
, the definite integral becomes:
Compare with FourierCosTransform:
Use Asymptotic to compute an asymptotic approximation:
FourierCosTransform and InverseFourierCosTransform are mutual inverses:
Results from FourierCosTransform and FourierTransform agree for even functions:
Possible Issues (1)
The result from an inverse Fourier cosine transform may not have the same form as the original:
Fourier cosine transform may be given in terms of generalized functions such as DiracDelta:
Tech Notes
Related Guides
History
Introduced in 1999 (4.0) | Updated in 2025 (14.2)
Text
Wolfram Research (1999), FourierCosTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierCosTransform.html (updated 2025).
CMS
Wolfram Language. 1999. "FourierCosTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/FourierCosTransform.html.
APA
Wolfram Language. (1999). FourierCosTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierCosTransform.html
BibTeX
@misc{reference.wolfram_2025_fouriercostransform, author="Wolfram Research", title="{FourierCosTransform}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/FourierCosTransform.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_fouriercostransform, organization={Wolfram Research}, title={FourierCosTransform}, year={2025}, url={https://reference.wolfram.com/language/ref/FourierCosTransform.html}, note=[Accessed: 28-February-2026]}