FrenetSerretSystem

FrenetSerretSystem[{x1,…,xn},t]

パラメトリック曲線 xi[t]の，一般化された曲率とフレネ・セレ(Frenet–Serret)基底を与える．

FrenetSerretSystem[{x1,…,xn},t,chart]

xiを指定された座標チャートの座標として解釈する．

詳細

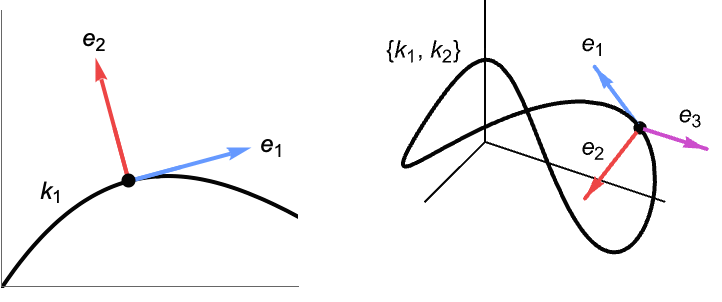
  • FrenetSerretSystemは{{k1,…,kn-1},{e1,…,en}}を返す．ただし，kiは一般化された曲率であり，eiはフレネ・セレの基底ベクトルである．
  • 第1基底ベクトル e1は，曲線の単位接線である．続く各ベクトルは，直前のベクトルに正規直交する派生ベクトルである．最後のベクトルは，右正規直交基底を完成するために選ばれる．
  • 派生ベクトルのいずれか1つがゼロの場合は，他のベクトルもゼロであるとみなされる．
  • 二次元および三次元における一般的な名前
  • {{k1},{e1,e2}}符号付きの曲率，接線，および法線
    {{k1,k2},{e1,e2,e3}}曲率，ねじれ，接線，法線，および従法線
  • FrenetSerretSystem[x,t]では，x がスカラー式の場合は，FrenetSerretSystemがパラメトリック曲線{t,x}の曲率を与える．
  • グラフが指定されている場合は，基底ベクトル eiはそのグラフに関連する正規直交基底で表現される．
  • FrenetSerretSystemの第3引数にある座標チャートは，CoordinateChartDataの第1引数におけるのと同じように{coordsys,metric,dim}で指定することができる．dim を省略した短縮形を使うこともできる．

例題

すべて開くすべて閉じる

例  (2)

二次元における円の曲率，接線，および法線：

円柱座標で表現された螺線の曲率，ねじれ，および関連の基底：

スコープ  (6)

直線は退化しているので，基底が零ベクトルで充填される：

平面に限定された螺線の曲率，ねじれ，関連の基底：

放物線 の単位法線と接線を構築する：

測定基準，座標系，パラメータを指定するフレネ・セレの系：

非零の接線，法線，従法線，tri法線：

FrenetSerretSystemは曲面空間に使うことができる：

アプリケーション  (3)

2つの空間曲線が平面で交わるかどうかを，両者の従法線の等価性を検討することで求める：

ユークリッド空間内の2本の曲線は，両者の曲率が弧長の関数として等しいときかつそのときに限り，剛体運動でオーバーレイすることができる：

パラメータ化すると，これらの曲線の曲率は異なるように見える：

しかし，曲率を弧長によって再度表現すると，これらの曲線が剛体運動によって関連していることが分かる：

接触円を作る．これは，ある点でこの曲線を最もよく近似する：

接触円の半径は曲率に反比例する：

円の中心は，接触点において曲線の法線に沿って置かれる：

曲線を2つの接触円および接触点とともにプロットする：

特性と関係  (7)

次元 では，最初の の曲率は，常に非負であるが，最後の曲率は負である：

二次元では，曲率に符号が付く：

三次元以上では，ArcCurvatureが最初の一般化された曲率である：

二次元では，ArcCurvatureは1つの一般化された曲率の絶対値である：

二次元では，法線は接線に対して常に反時計回りに回転する：

曲線が三次元空間に埋め込まれた場合，法線はどちらの方向に回転することもできる：

方向転換は曲率がゼロと交差したときに起る：

法線および従法線は，交差においては定義されておらず，方向が反転される：

ユークリッド空間では，最後の曲率が0と等しくさえあれば，その曲線は超平面内にある：

超平面は最後の基底ベクトル（この場合は従法線）と直交する：

曲線を含む平面を，曲線上の点とその点における接線と法線を使ってプロットする：

曲線，超平面，従法線：

非平面の曲面に埋込まれた曲線の場合，接線以外の基底ベクトルは，曲面に対して一定の角度を保つ必要はない：

インタラクティブな例題  (1)

ある関数のプロットが単位接線および単位法線とともに示してある．点をクリックすると，その点の単位接線と単位法線を見ることができる：

おもしろい例題  (1)

曲線に沿って動く，接線，法線，従法線のアニメーションを伴った三つ葉結び目：

Wolfram Research (2014), FrenetSerretSystem, Wolfram言語関数， https://reference.wolfram.com/language/ref/FrenetSerretSystem.html.

テキスト

Wolfram Research (2014), FrenetSerretSystem, Wolfram言語関数， https://reference.wolfram.com/language/ref/FrenetSerretSystem.html.

CMS

Wolfram Language. 2014. "FrenetSerretSystem." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FrenetSerretSystem.html.

APA

Wolfram Language. (2014). FrenetSerretSystem. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FrenetSerretSystem.html

BibTeX

@misc{reference.wolfram_2024_frenetserretsystem, author="Wolfram Research", title="{FrenetSerretSystem}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/FrenetSerretSystem.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_frenetserretsystem, organization={Wolfram Research}, title={FrenetSerretSystem}, year={2014}, url={https://reference.wolfram.com/language/ref/FrenetSerretSystem.html}, note=[Accessed: 22-November-2024 ]}