FrequencySamplingFilterKernel

FrequencySamplingFilterKernel[{a1,…,ak}]

creates a finite impulse response (FIR) filter kernel using a frequency sampling method from amplitude values ai.

FrequencySamplingFilterKernel[{a1,…,ak},m]

creates an FIR filter kernel of type m.

Details and Options

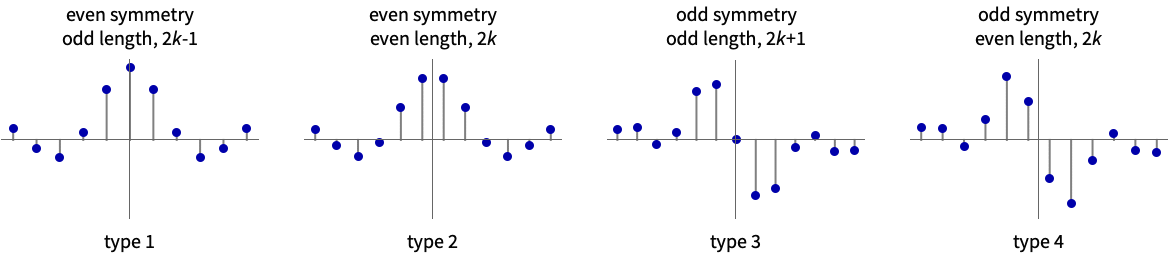
  • Possible types m for FIR filters created for a list {a1,a2,…,ak} of amplitudes are:
  • The default type is .
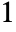  • The frequency sampling method uniformly samples the frequency domain from 0 to .
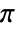  • FrequencySamplingFilterKernel by default uses a sampling of the frequency domain at integer multiples of 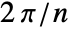, where 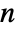is the length of the filter. With "Shifted"->True, the frequencies are shifted from 0 by . »
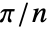  • Amplitude values should be non-negative. Typically, values ai=0 specify a stopband, and values ai=1 specify a passband.
  • The kernel ker returned by FrequencySamplingFilterKernel can be used in ListConvolve[ker,data] to apply the filter to data.
  • FrequencySamplingFilterKernel takes a WorkingPrecision option that specifies the precision to use in internal computations. The default setting is WorkingPrecision->MachinePrecision.

Examples

open allclose all

Basic Examples  (1)

A symmetric odd-length FIR lowpass kernel:

Scope  (7)

A type 1 FIR kernel with even symmetry and odd length:

A type 2 FIR kernel with even symmetry and even length:

A type 3 FIR kernel with odd symmetry and odd length:

A type 4 FIR kernel with odd symmetry and even length:

A symmetric odd-length FIR highpass kernel:

A symmetric even-length FIR bandpass kernel:

A full-band differentiator FIR kernel:

Options  (1)

"Shifted"  (1)

By default, first frequency is sampled at 0:

With "Shifted"->True, first frequency is offset from 0 by :

Applications  (2)

Smooth data by convolving it with a lowpass filter kernel:

Apply a derivative filter to rows of an image:

Properties & Relations  (1)

Apply a window to an FIR filter to reduce ripple in its magnitude response:

Wolfram Research (2012), FrequencySamplingFilterKernel, Wolfram Language function, https://reference.wolfram.com/language/ref/FrequencySamplingFilterKernel.html.

Text

Wolfram Research (2012), FrequencySamplingFilterKernel, Wolfram Language function, https://reference.wolfram.com/language/ref/FrequencySamplingFilterKernel.html.

CMS

Wolfram Language. 2012. "FrequencySamplingFilterKernel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FrequencySamplingFilterKernel.html.

APA

Wolfram Language. (2012). FrequencySamplingFilterKernel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FrequencySamplingFilterKernel.html

BibTeX

@misc{reference.wolfram_2025_frequencysamplingfilterkernel, author="Wolfram Research", title="{FrequencySamplingFilterKernel}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/FrequencySamplingFilterKernel.html}", note=[Accessed: 22-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_frequencysamplingfilterkernel, organization={Wolfram Research}, title={FrequencySamplingFilterKernel}, year={2012}, url={https://reference.wolfram.com/language/ref/FrequencySamplingFilterKernel.html}, note=[Accessed: 22-February-2025 ]}