FrequencySamplingFilterKernel

FrequencySamplingFilterKernel[{a1,…,ak}]

振幅の値 aiから周波数サンプリング法を使って有限インパルス応答(FIR)フィルタカーネルを作る．

FrequencySamplingFilterKernel[{a1,…,ak},m]

タイプ m のFIRフィルタカーネルを作る．

詳細とオプション

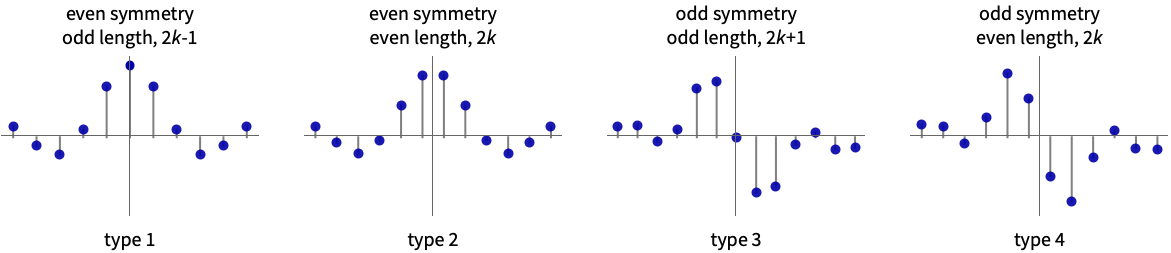
  • 振幅のリスト{a1,a2,…,ak}から作るFIRフィルタの可能なタイプ m
  • デフォルトタイプは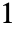である．
  • 周波数サンプリング法は0から 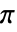までの周波数領域を一様にサンプリングする．
  • FrequencySamplingFilterKernelは，デフォルトで，整数を 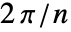倍した周波数領域でサンプリングを行う．ただし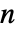， はフィルタの長さである．"Shifted"->Trueとすると，周波数は0から 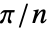シフトされる． »
  • 周波数の値は非負でなければならない．一般に，値 ai=0でストップバンドを，値 ai=1でパスバンドを指定する．
  • FrequencySamplingFilterKernelによって返されるカーネル ker をListConvolve[ker,data]で使ってフィルタを data に適用することができる．
  • FrequencySamplingFilterKernelは，内部計算で使う精度を指定するWorkingPrecisionオプションを取る．デフォルト設定はWorkingPrecision->MachinePrecisionである．

例題

すべて開くすべて閉じる

例  (1)

対称で長さが奇数のFIRローパスカーネル：

スコープ  (7)

偶対称で長さが奇数のタイプ1のFIRカーネル：

偶対称で長さが偶数のタイプ2のFIRカーネル：

奇対称で長さが奇数のタイプ3のFIRカーネル：

奇対称で長さが偶数のタイプ4のFIRカーネル：

対称で長さが奇数のFIRハイパスカーネル：

対称で長さが偶数のFIRバンドパスカーネル：

充満帯微分器FIRカーネル：

オプション  (1)

"Shifted"  (1)

デフォルトで，最初の周波数は0でサンプルされる：

"Shifted"->Trueとすると，最初の周波数は0からのオフセットになる：

アプリケーション  (2)

ローパスフィルタカーネルでたたみ込むことでデータを平滑化する：

画像の行に導関数フィルタを適用する：

特性と関係  (1)

FIRフィルタに窓を適用して振幅特性の波を減らす：

Wolfram Research (2012), FrequencySamplingFilterKernel, Wolfram言語関数， https://reference.wolfram.com/language/ref/FrequencySamplingFilterKernel.html.

テキスト

Wolfram Research (2012), FrequencySamplingFilterKernel, Wolfram言語関数， https://reference.wolfram.com/language/ref/FrequencySamplingFilterKernel.html.

CMS

Wolfram Language. 2012. "FrequencySamplingFilterKernel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FrequencySamplingFilterKernel.html.

APA

Wolfram Language. (2012). FrequencySamplingFilterKernel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FrequencySamplingFilterKernel.html

BibTeX

@misc{reference.wolfram_2024_frequencysamplingfilterkernel, author="Wolfram Research", title="{FrequencySamplingFilterKernel}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/FrequencySamplingFilterKernel.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_frequencysamplingfilterkernel, organization={Wolfram Research}, title={FrequencySamplingFilterKernel}, year={2012}, url={https://reference.wolfram.com/language/ref/FrequencySamplingFilterKernel.html}, note=[Accessed: 22-November-2024 ]}