WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

FromFiniteField

FromFiniteField[a,ff]

有限体 ff の素部分体の元 a を整数に変換する．

FromFiniteField[expr,ff,t]

有理式 expr の係数中の有限体 ff の元を t についての多項式に変換する．ただし，t は体の生成元を表す．

詳細

FromFiniteFieldは，ff の元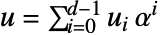を置換する．ただし，α=ff[{0,1}]は多項式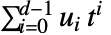を持つ体の生成元である．
FromFiniteFieldは，expr のList，Plus，Timesおよび整数のPowerに入る．

例題

すべて開くすべて閉じる

例 (4)

有限体の素部分体の元を整数に変換する：

有限体の元を体の生成元を表す変数の多項式に変換する：

有理式の素体の係数を整数に変換する：

有理式における有限体の係数を変数が体の生成元を表す多項式に変換する：

スコープ (3)

有限体の素部分体の元を整数に変換する：

b は素部分体の元ではない：

有限体の元を体の生成元を表す変数の多項式に変換する：

有理式における有限体の係数を体の生成元の多項式に変換する：

特性と関係 (2)

ToFiniteFieldは係数を有限体の元に変換する．t は体の生成元を表す：

FiniteFieldIndexは体の元の指数を与える：

FromFiniteFieldは素部分体の元についてのみ整数を与える：

トップへ