FromPolarCoordinates[{r,θ}]
gives the {x,y} Cartesian coordinates corresponding to the polar coordinates {r,θ}.
FromPolarCoordinates[{r,θ1,…,θn-2,ϕ}]
gives the coordinates corresponding to the hyperspherical coordinates {r,θ1,…,θn-2,ϕ}


FromPolarCoordinates
FromPolarCoordinates[{r,θ}]
gives the {x,y} Cartesian coordinates corresponding to the polar coordinates {r,θ}.
FromPolarCoordinates[{r,θ1,…,θn-2,ϕ}]
gives the coordinates corresponding to the hyperspherical coordinates {r,θ1,…,θn-2,ϕ}
Details

- FromPolarCoordinates converts points in the standard range
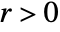 ,
, 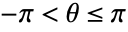 in two dimensions and
in two dimensions and 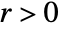 ,
, 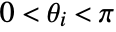 ,
, 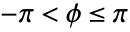 in higher dimensions.
in higher dimensions. - FromPolarCoordinates automatically threads over arrays of coordinate lists.
Examples
open all close allBasic Examples (3)
Properties & Relations (6)
FromPolarCoordinates checks that inputs obey the normal restrictions of polar coordinates:
This point violates the condition on the angle ![]() :
:
Extract the symbolic transform from CoordinateTransformData to apply it to singular points:
FromPolarCoordinates preserves the shape of arrays:
FromPolarCoordinates[pt] is a special case of CoordinateTransform:
FromPolarCoordinates inverts ToPolarCoordinates:
FromPolarCoordinates[{x,y,z}] uses spherical coordinates about the ![]() axis:
axis:
FromSphericalCoordinates[{x,y,z}] uses spherical coordinates about the ![]() axis:
axis:
FromPolarCoordinates changes the coordinate values of points:
TransformedField changes the coordinate expressions for fields:
Related Guides
History
Text
Wolfram Research (2015), FromPolarCoordinates, Wolfram Language function, https://reference.wolfram.com/language/ref/FromPolarCoordinates.html.
CMS
Wolfram Language. 2015. "FromPolarCoordinates." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FromPolarCoordinates.html.
APA
Wolfram Language. (2015). FromPolarCoordinates. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FromPolarCoordinates.html
BibTeX
@misc{reference.wolfram_2025_frompolarcoordinates, author="Wolfram Research", title="{FromPolarCoordinates}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FromPolarCoordinates.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_frompolarcoordinates, organization={Wolfram Research}, title={FromPolarCoordinates}, year={2015}, url={https://reference.wolfram.com/language/ref/FromPolarCoordinates.html}, note=[Accessed: 03-March-2026]}