Function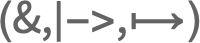

body& 或 Function[body]

是一个纯（或“匿名”）函数. 形式参数是 #（或 #1）、#2 等.

x|->body 或者 xbody 或者 Function[x,body]

是一个具有简单形式参数 x 的纯函数.

{x1,x2,…}|->body 或者 {x1,x2,…}body 或者 Function[{x1,x2,…},body]

是一个具有形式参数列表的纯函数.

Function[params,body,attrs]

是一个纯函数，在计算时被认为具有属性 attrs.

更多信息

  • 当 Function[body] 或 body& 用到参数集合上时，#（或 #1）由第一个参数代替，#2 由第二个代替，以此类推. #0 由函数本身代替.
  • 如果给出的参数比函数中 # i 数目更多的话，剩余的参数被忽略. »
  • ## 表示提供的所有参数的序列. »
  • ## n 表示从数字 n 开始的参数. »
  • 当应用于相关性时，#name 等价于 #["name"]，并且挑选相关性中的元素.
  • 在格式 #name 中，name 中的字符可以是不以数字开始的任意字母数字组合.
  • 用 |->、fn 或 \[Function] 键入符号 .
  • Function 与 LISP 或形式逻辑中的 λ 类似.
  • Function 有属性 HoldAll. 仅在形式参数被自变量替换后计算函数体.
  • Function[{x1,…},body] 中已命名的形式参数 xi 视为局部变量处理，并当需要避免和提供给函数的实际自变量混淆时，被重命名为 xi$. »
  • Function 结构可以以任意方式嵌套. 每种方式都可以当作作用域结构处理，如果有必要，已命名的内部变量被重命名. »
  • 在 Function[params, body, attrs] 中，attrs 可以是一个属性或属性列表. »
  • Function[Null,body,attrs] 表示一个函数，用 # 等给出 body 内的参数.

范例

打开所有单元关闭所有单元

基本范例  (4)

具有一个参数的纯函数：

具有两个参数的纯函数：

将 设置为一个纯函数：

用纯函数：

从一个相关性中提取已命名参数：

范围  (15)

把纯函数用作变量  (5)

将纯函数映射到列表：

用纯函数选择：

将纯函数作为一个谓词使用：

从纯函数中创建一个数组：

比较每个元素的第二部分，以进行排序：

把纯函数用作选项值  (3)

在 FixedPoint 中指定一个自定义的比较函数：

指定一个自定义的颜色函数：

提供一个自定义的距离函数：

将一个纯函数作为结果返回  (4)

纯函数的导数：

Tan 的导数：

微分方程的解可能表示为一个纯函数：

微分方程可能返回纯函数：

函数和相关性  (3)

#name 是 #["name"] 的缩略格式：

#name 指的是第一个参数中的相关性：

从一个相关性插口而不是第一个提取：

推广和延伸  (4)

## 表示所有参数：

## n 表示从 n 开始的自变量：

创建一个具有 Listable 属性的纯函数：

#0 表示整个纯函数：

使用 #0 的阶乘递归定义：

应用  (3)

将一个带有若干个参数的函数转化为带有一个参数列表的函数：

一个函数，返回其自变量乘以 n 的函数：

以未计算的形式保留参数：

属性和关系  (11)

#1 仅使用提供的第一个自变量；其余的被忽略：

在一个常量纯函数中，不使用任何自变量结果：

可在纯函数内部完成替换：

当有干扰的可能时，形式参数被重命名：

参数的名称没有关系：

当然，重新使用一个名称来引入一个新的范围：

嵌套函数每次取一个参数：

在单变量情况下，f[#]& 与简单的 f 相同：

通常 f[##]& 与 f 相同：

将关于变量 的公式转换为一个纯函数：

在 Table 中使用一个公式：

在相等的 Array 表达式中，用相应的纯函数：

特殊目的的函数结构包括 InterpolatingFunction：

CompiledFunction：

NearestFunction：

LinearSolveFunction：

可能存在的问题  (4)

& 的绑定较 -> 宽松，所以它通常需要在规则中使用圆括号：

& 的绑定较 ? 宽松，所以它通常需要在模式测试中使用圆括号：

Function 直到函数被应用才计算它的函数体：

提供的参数小于所需参数的数目时，会产生错误：

巧妙范例  (2)

定义一个递归理论的递归运算符 [更多信息]：

用它来定义阶乘函数：

将牛顿公式用于求函数的零点：

Wolfram Research (1988)，Function，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Function.html （更新于 2020 年）.

文本

Wolfram Research (1988)，Function，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Function.html （更新于 2020 年）.

CMS

Wolfram 语言. 1988. "Function." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/Function.html.

APA

Wolfram 语言. (1988). Function. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Function.html 年

BibTeX

@misc{reference.wolfram_2024_function, author="Wolfram Research", title="{Function}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/Function.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_function, organization={Wolfram Research}, title={Function}, year={2020}, url={https://reference.wolfram.com/language/ref/Function.html}, note=[Accessed: 22-November-2024 ]}