Slot

#

represents the first argument supplied to a pure function.

#n

represents the n ^(th) argument.

#name

represents the value associated with key "name" in an association in the first argument.

Details

  • # is used to represent arguments or formal parameters in pure functions of the form body& or Function[body].
  • # is equivalent to Slot[1].
  • #n is equivalent to Slot[n]. n must be a non‐negative integer.
  • #0 gives the head of the function, i.e. the pure function itself.
  • When applied to an association, #name is equivalent to #["name"] and picks out elements in the association.
  • In the form #name, the characters in name can be any combination of alphanumeric characters not beginning with digits.

Background & Context

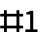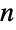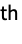
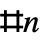  • Slot[1] represents the first argument supplied to a pure function. The expression Slot[1] may be compactly denoted with the hash character #, or more explicitly as #1. The ^(th) argument to a pure function is represented by Slot[n], commonly denoted 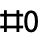#n. The zeroth slot 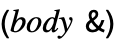#0 of a pure function is its head.
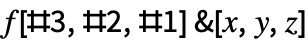  • Slot is typically used inside Function. In pure functions of the form (body &), # is used as part of the body to represent arguments or formal parameters. An example application of Slot is given by f[#3,#2,#1]&[x,y,z], which evaluates to f[z,y,x].
  • A sequence of arguments to be supplied to a pure function is represented using SlotSequence (written in shorthand as ##n).
  • When pure functions are nested, the meaning of slots may become ambiguous, in which case parameters must be specified using an explicit Function construction with named parameters.

Examples

open allclose all

Basic Examples  (3)

# represents the first argument of a pure function:

Use numbered arguments:

Used named arguments from an association:

Scope  (5)

# is short for #1, the first argument:

#name is effectively a short form of #["name"]:

#name is interpreted as Slot["name"]:

#name always refers to the association in the first argument:

Extract from an association slot other than the first:

Generalizations & Extensions  (1)

#0 stands for the whole pure function:

Applications  (1)

Programmatically create a pure function of 5 arguments:

Properties & Relations  (3)

# allows function arguments to be referenced without giving them names:

Additional arguments are ignored:

## stands for the sequence of all arguments:

Possible Issues  (3)

Use explicit names to set up nested pure functions:

Use # for the inner function:

Use # for the outer function:

Using nested # notation behaves differently:

If too few arguments are provided, a message is generated:

A space between # and the following token will be interpreted as multiplication:

Neat Examples  (1)

A recursive definition for factorial using #0:

Wolfram Research (1988), Slot, Wolfram Language function, https://reference.wolfram.com/language/ref/Slot.html (updated 2014).

Text

Wolfram Research (1988), Slot, Wolfram Language function, https://reference.wolfram.com/language/ref/Slot.html (updated 2014).

CMS

Wolfram Language. 1988. "Slot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Slot.html.

APA

Wolfram Language. (1988). Slot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Slot.html

BibTeX

@misc{reference.wolfram_2024_slot, author="Wolfram Research", title="{Slot}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Slot.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_slot, organization={Wolfram Research}, title={Slot}, year={2014}, url={https://reference.wolfram.com/language/ref/Slot.html}, note=[Accessed: 22-December-2024 ]}