finds the discontinuities of ![]() for x∈Reals.
for x∈Reals.
FunctionDiscontinuities[f,x,dom]
finds the discontinuities of ![]() for x∈dom.
for x∈dom.
FunctionDiscontinuities[{f1,f2,…},{x1,x2,…},dom]
finds the discontinuities of ![]() for x1,x2,…∈dom.
for x1,x2,…∈dom.


FunctionDiscontinuities
finds the discontinuities of ![]() for x∈Reals.
for x∈Reals.
FunctionDiscontinuities[f,x,dom]
finds the discontinuities of ![]() for x∈dom.
for x∈dom.
FunctionDiscontinuities[{f1,f2,…},{x1,x2,…},dom]
finds the discontinuities of ![]() for x1,x2,…∈dom.
for x1,x2,…∈dom.
Details
- Function discontinuities are typically used to either find regions where a function is guaranteed to be continuous or to find points and curves where special analysis needs to be performed.
- FunctionDiscontinuities gives an implicit description of a set
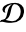 such that
such that 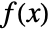 is continuous in
is continuous in 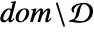 . The set
. The set 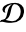 is not guaranteed to be minimal.
is not guaranteed to be minimal. - The resulting implicit description consists of equations, inequalities, domain specifications and logical combinations of these suitable for use in functions such as Reduce and Solve, etc.
- Possible values for dom are Reals and Complexes.
Examples
open all close allBasic Examples (4)
Scope (5)
Discontinuities of a real univariate function:
Find the discontinuity points between ![]() and
and ![]() :
:
Visualize the discontinuities:
Discontinuities of a function composition:
Find a finite set of discontinuity points between ![]() and
and ![]() :
:
Visualize the discontinuities:
Discontinuities over the reals include the points where the function is not real valued:
Discontinuities of a complex univariate function:
Compute the discontinuities in terms of Re[z] and Im[z]:
Visualize the discontinuities:
Applications (6)
Basic Applications (4)
Find the discontinuity points between ![]() and
and ![]() :
:
Visualize the discontinuities:
Show that there are no discontinuities:
Find the discontinuities of the complex function ![]() :
:
Compute the discontinuities in terms of Re[z] and Im[z]:
Visualize the discontinuities:
Find the discontinuities of ![]() given the discontinuities of
given the discontinuities of ![]() and
and ![]() :
:
Suppose the discontinuities of ![]() and
and ![]() are contained in solution sets of
are contained in solution sets of ![]() and
and ![]() :
:
The discontinuities of ![]() are contained in the solution set of
are contained in the solution set of ![]() :
:
Calculus (1)
Visualization (1)
Use discontinuities to find Exclusions settings for Plot:
Convert the discontinuities into the format required by Exclusions:
Use the exclusions in Plot:
Properties & Relations (2)
The function is continuous outside the set given by FunctionDiscontinuities:
Use FunctionContinuous to check the continuity:
FunctionSingularities gives a set outside which the function is analytic:
The set of discontinuities is a subset of the set of singularities:
Related Guides
History
Text
Wolfram Research (2020), FunctionDiscontinuities, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionDiscontinuities.html.
CMS
Wolfram Language. 2020. "FunctionDiscontinuities." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionDiscontinuities.html.
APA
Wolfram Language. (2020). FunctionDiscontinuities. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionDiscontinuities.html
BibTeX
@misc{reference.wolfram_2025_functiondiscontinuities, author="Wolfram Research", title="{FunctionDiscontinuities}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionDiscontinuities.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_functiondiscontinuities, organization={Wolfram Research}, title={FunctionDiscontinuities}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionDiscontinuities.html}, note=[Accessed: 28-February-2026]}