finds the singularities of ![]() for x∈Reals.
for x∈Reals.
FunctionSingularities[f,x,dom]
finds the singularities of ![]() for x∈dom.
for x∈dom.
FunctionSingularities[{f1,f2,…},{x1,x2,…},dom]
finds the singularities of ![]() for x1,x2,…∈dom.
for x1,x2,…∈dom.


FunctionSingularities
finds the singularities of ![]() for x∈Reals.
for x∈Reals.
FunctionSingularities[f,x,dom]
finds the singularities of ![]() for x∈dom.
for x∈dom.
FunctionSingularities[{f1,f2,…},{x1,x2,…},dom]
finds the singularities of ![]() for x1,x2,…∈dom.
for x1,x2,…∈dom.
Details


- Function singularities are typically used to either find regions where a function is guaranteed to be analytic or to find points and curves where special analysis needs to be performed.
- FunctionSingularities gives an implicit description of a set
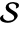 such that
such that 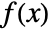 is analytic in
is analytic in 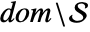 . The set
. The set 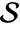 is not guaranteed to be minimal.
is not guaranteed to be minimal. - The resulting implicit description consists of equations, inequalities, domain specifications and logical combinations of these suitable for use in functions such as Reduce and Solve, etc.
- There are several sources for singularities, including Laurent series representation, multivalued functions, and piecewise and partial definitions of functions.
- Singularities from the Laurent series representation
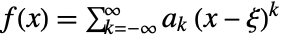 where
where 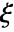 is the location of the isolated singularity:
is the location of the isolated singularity: -
removable singularity 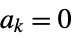 for
for 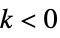 , e.g.
, e.g. 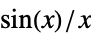 for
for 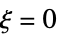
pole singularity 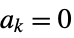 for
for 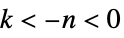 , e.g.
, e.g. 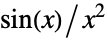 for
for 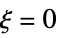
essential singularity 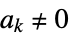 for infinitely many
for infinitely many 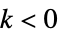 , e.g.
, e.g. 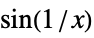 for
for 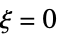
inessential singularity a pole or removable singularity - Singularities coming from the selection of principal branches of multivalued functions:
-
branch point point where branches of a multivalued function come together, e.g. 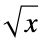 for
for 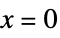
branch cut curve along which a function is discontinuous in order to get a single valued function, e.g. 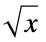 for
for 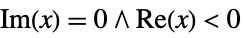
- Singularities coming from piecewise-defined functions or natural domain of definition:
-
piecewise piecewise defined function, e.g. 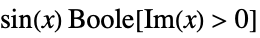 for
for 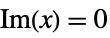
domain of definition complement of domain of definition, e.g. ![TemplateBox[{1, {1, /, 2}, x}, EllipticTheta] TemplateBox[{1, {1, /, 2}, x}, EllipticTheta]](Files/FunctionSingularities.en/28.png) for
for ![TemplateBox[{x}, Abs]>=1 TemplateBox[{x}, Abs]>=1](Files/FunctionSingularities.en/29.png)
- For a multivariate function, the singularities are taken to be the singularities for each variable separately.
- Possible values for dom are Reals and Complexes.
Examples
open all close allBasic Examples (4)
Scope (5)
Singularities of a real univariate function:
Find the singular points between ![]() and
and ![]() :
:
Singularities of a function composition:
Find the singular points between ![]() and
and ![]() :
:
Singularities over the reals include the points where the function is not real valued:
Singularities of a complex univariate function:
Compute the singularities in terms of Re[z] and Im[z]:
Applications (6)
Basic Applications (5)
Find the singular points between ![]() and
and ![]() :
:
Find the singular points between ![]() and
and ![]() :
:
The function ![]() is continuous but not analytic:
is continuous but not analytic:
Show that there are no singularities:
Find the singularities of the complex function ![]() :
:
Compute the singularities in terms of Re[z] and Im[z]:
Find the singularities of ![]() given the singularities of
given the singularities of ![]() and
and ![]() :
:
Suppose the singularities of ![]() and
and ![]() are contained in solution sets of
are contained in solution sets of ![]() and
and ![]() :
:
Properties & Relations (3)
The function is analytic outside the set given by FunctionSingularities:
Use FunctionAnalytic to check the analyticity:
FunctionDiscontinuities gives a set outside which the function is continuous:
The set of discontinuities is a subset of the set of singularities:
FunctionSingularities finds a condition satisfied by all singularities:
Use SolveValues to find the singularities:
Use FunctionPoles to find the pole singularities and their multiplicities:
Related Guides
History
Text
Wolfram Research (2020), FunctionSingularities, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionSingularities.html.
CMS
Wolfram Language. 2020. "FunctionSingularities." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionSingularities.html.
APA
Wolfram Language. (2020). FunctionSingularities. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionSingularities.html
BibTeX
@misc{reference.wolfram_2025_functionsingularities, author="Wolfram Research", title="{FunctionSingularities}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionSingularities.html}", note=[Accessed: 18-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_functionsingularities, organization={Wolfram Research}, title={FunctionSingularities}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionSingularities.html}, note=[Accessed: 18-January-2026]}