WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

GPUArray
✖
GPUArray

Unsupported in CloudNew in 14.2[Experimental]

✖
GPUArray[array]

yields an array stored in memory accessible for GPU-accelerated computation.

Details

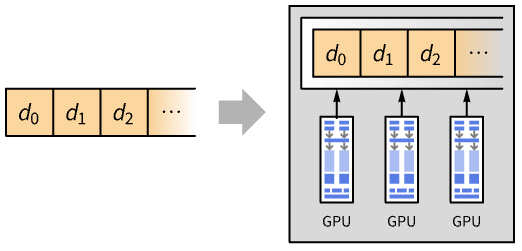
  • GPUArray provides an efficient representation for storing and manipulating data accessible from a graphics processor unit (GPU).
  • GPUArray is typically used to enhance speed of execution of functions by running computations on the GPU.
  • GPUArray[array] creates an array in GPU memory or unified memory.
  • The array can have the following forms:
  • {e1,…},{{e1,…},…},…full array of numeric elements
    NumericArray[…]numeric array of a specified type
  • Normal[GPUArray[array]] converts the GPUArray object to an ordinary list of values.
  • Additional conversions include:
  • SparseArray[GPUArray[…]]sparse array with few nonzero elements
    NumericArray[GPUArray[…],type]numeric array of a specified type
  • Information for a GPUArray includes the following properties:
  • "ElementType"element native type
    "Dimensions"list of the dimensions
  • Functions such as LinearSolve, Plus and Part work on GPUArray by running the computation on the GPU.
  • GPUArray is treated as a raw object by functions like AtomQ and for purposes of pattern matching.

Examples

open allclose all

Basic Examples  (1)Summary of the most common use cases

Create a GPUArray object from a vector:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-l5j4o6
Out[1]=1

Compute the cosine:

In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-tvztwb
Out[2]=2

Converts to an ordinary list of values:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-7namgu
Out[3]=3

Scope  (27)Survey of the scope of standard use cases

Basic Uses  (4)

Create a GPUArray object from a vector:

In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-p750xp
Out[2]=2

From a matrix:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-gdslw7
Out[3]=3

Use NumericArray to create a GPUArray object of a specified type:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-wwfq5o
Out[1]=1

64-bit integers:

In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-2isqpt
Out[2]=2

Convert a GPUArray object to an ordinary list of values:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-rl036m
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-bn80ro
Out[2]=2

Convert to a NumericArray object:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-e5hv08
Out[3]=3

Convert to a SparseArray:

In[4]:=4
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-t17og5
Out[4]=4

Get information of a GPUArray object:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-z89d97
Out[1]=1

Dimensions:

In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-026nzt
Out[2]=2

Type of elements:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-c9c8oy
Out[3]=3

Arrays Operations  (3)

Test whether a GPUArray object is a vector:

In[5]:=5
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-6cl86j
Out[5]=5
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-b0p9yq
Out[2]=2

A matrix:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-wcfeqj
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-9hk3pn
Out[4]=4

Extract parts of a GPUArray object:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-o8tqxh
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-il6kqi
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-ejfu1x
Out[3]=3

Get properties of a GPUArray object:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-5u7t61
Out[1]=1

Dimensions:

In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-o6e3ph
Out[2]=2

Depth:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-4mehnu
Out[3]=3

Byte count:

In[4]:=4
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-cdxj4e
Out[4]=4

Mathematical Operations  (6)

Apply arithmetic operations on GPUArray objects:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-k3e2w6

Addition:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-hxj29h
Out[3]=3

Multiplication:

In[4]:=4
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-tb2mnt
Out[4]=4

Power:

In[5]:=5
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-n8d9cf
Out[5]=5

Evaluate numerically trigonometric functions:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-57vl0j

Sine:

In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-mh4j3v
Out[2]=2

Cosine:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-32e7fa
Out[3]=3

Arc cosine:

In[4]:=4
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-qtqlkt
Out[4]=4

Compute transcendental functions:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-6uf2mt

Exp:

In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-z2ecn7
Out[2]=2

Log:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-h577v2
Out[3]=3

Power:

In[4]:=4
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-gkhdti
Out[4]=4

Evaluate efficiently hyperbolic functions:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-h7ifzq

Sinh:

In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-tc6jpw
Out[2]=2

Cosh:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-dftjmy
Out[3]=3

Inverse cosine:

In[4]:=4
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-5hvsor
Out[4]=4

Evaluate numerically integer functions:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-r1ws44

Ceiling:

In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-iby14n
Out[2]=2

Floor:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-u0q8jp
Out[3]=3

Round:

In[4]:=4
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-sqxofj
Out[4]=4

Compute absolute values and signs functions:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-b4mc85

Abs:

In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-vs3jfb
Out[2]=2

Sign:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-4bkbw7
Out[3]=3

Absolute value of the real:

In[4]:=4
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-vi8z1j
Out[4]=4

Fourier Analysis  (2)

Find a discrete Fourier transform:

In[10]:=10
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-y5k9fh
Out[10]=10
In[11]:=11
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-hgadzl
Out[11]=11

Inverse Fourier transform of a complex list:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-uqjook
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-3ixiw
Out[2]=2

Statistics  (3)

Evaluate statistics functions on a GPUArray object:

In[11]:=11
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-hneams

Mean:

In[12]:=12
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-1kms00
Out[12]=12

Geometric mean:

In[13]:=13
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-wxs7n9
Out[13]=13

Variance:

In[14]:=14
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-fx5ceu
Out[14]=14

Standard deviation:

In[15]:=15
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-7y0uch
Out[15]=15

Skewness:

In[16]:=16
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-dm1qv6
Out[16]=16

Minimum of a GPUArray object:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-koitlu
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-s7tw94
Out[2]=2

Maximum:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-i2eai
Out[3]=3

Minimum and maximum:

In[4]:=4
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-b4bo1o
Out[4]=4

Sort a GPUArray object:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-r824ij
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-82d68y
Out[2]=2

Linear Algebra  (4)

Apply matrix operations on GPUArray objects:

In[8]:=8
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-c9db14

Dot product:

In[6]:=6
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-xp4i1j
Out[6]=6

Transpose:

In[7]:=7
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-wso8f
Out[7]=7

Trace:

In[10]:=10
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-nocedq
Out[10]=10

Solve a matrix-vector equation:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-34r86w
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-6d9hq7
In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-o45667
Out[3]=3

A matrix equation:

In[4]:=4
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-e1lfch
In[5]:=5
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-6p4cba
In[6]:=6
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-s9d5id
Out[6]=6

Solve a matrix-vector least-squares problem:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-pokusj
Out[1]=1

Solve a matrix-matrix least-squares problem:

In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-w94h00
Out[2]=2

Compute the singular value decomposition of a complex-valued matrix:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-147kew
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-o2cjs9
Out[2]=2

Up to expected precision loss, m=u.sigma.TemplateBox[{v}, ConjugateTranspose]:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-jaucil
Out[3]=3

Random Number Generation  (2)

Switch to the GPU random number generator:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-1q7ttr
Out[1]=1

Random numbers are now generated using it:

In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-15arzs
Out[2]=2

Random integers:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-hze96w
Out[3]=3

Random complexes:

In[4]:=4
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-nt3ciz
Out[4]=4

A specific seed will affect the current GPU random number generator:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-oc6p1d
Out[1]=1

Visualization  (3)

Plot a list of values from a continuous probability distribution:

In[7]:=7
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-dm2lt0
Out[7]=7
In[8]:=8
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-golww6
Out[8]=8

Plot an array of numbers:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-ti6xga
Out[1]=1

Plot a matrix as an array of colors:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-mdrf6
Out[1]=1

Properties & Relations  (4)Properties of the function, and connections to other functions

Use GPUArrayQ to test whether an object is a valid GPUArray object:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-e8l2yi
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-jv8l6b
Out[2]=2

Find the number of bytes used to store a GPUArray object:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-db690e
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-bazdgh
Out[2]=2

Use Normal to retrieve data from GPU:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-dgmwn
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-wvl9rh
Out[2]=2

GPUArray preserves representation types of elements in NumericArray objects:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-g3r1on
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-09ktkx
Out[2]=2

Element type:

In[3]:=3
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-mp7xlc
Out[3]=3

Possible Issues  (2)Common pitfalls and unexpected behavior

GPUArray autoevaluates if no supported GPUs were detected:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-5hmljm
Out[1]=1

Operations without GPU-accelerated support fall back to CPU implementations:

In[1]:=1
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-4qdni4
In[2]:=2
✖
https://wolfram.com/xid/0bh1s8b50ft0fi-q2717w
Out[2]=2
Wolfram Research (2025), GPUArray, Wolfram Language function, https://reference.wolfram.com/language/ref/GPUArray.html.
✖
Wolfram Research (2025), GPUArray, Wolfram Language function, https://reference.wolfram.com/language/ref/GPUArray.html.

Text

Wolfram Research (2025), GPUArray, Wolfram Language function, https://reference.wolfram.com/language/ref/GPUArray.html.

✖
Wolfram Research (2025), GPUArray, Wolfram Language function, https://reference.wolfram.com/language/ref/GPUArray.html.

CMS

Wolfram Language. 2025. "GPUArray." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GPUArray.html.

✖
Wolfram Language. 2025. "GPUArray." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GPUArray.html.

APA

Wolfram Language. (2025). GPUArray. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GPUArray.html

✖
Wolfram Language. (2025). GPUArray. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GPUArray.html

BibTeX

@misc{reference.wolfram_2025_gpuarray, author="Wolfram Research", title="{GPUArray}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/GPUArray.html}", note=[Accessed: 07-May-2025 ]}

✖
@misc{reference.wolfram_2025_gpuarray, author="Wolfram Research", title="{GPUArray}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/GPUArray.html}", note=[Accessed: 07-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_gpuarray, organization={Wolfram Research}, title={GPUArray}, year={2025}, url={https://reference.wolfram.com/language/ref/GPUArray.html}, note=[Accessed: 07-May-2025 ]}

✖
@online{reference.wolfram_2025_gpuarray, organization={Wolfram Research}, title={GPUArray}, year={2025}, url={https://reference.wolfram.com/language/ref/GPUArray.html}, note=[Accessed: 07-May-2025 ]}