GeoGridDirectionDifference

GeoGridDirectionDifference[proj,loc,β]

gives the difference between the angle from north to direction β on the geo grid obtained with projection proj and the actual angle from north to direction β at location loc.

GeoGridDirectionDifference[proj,loc,αβ]

gives the difference between projected and unprojected angles from direction α to direction β.

Details and Options

  • Geo grid direction difference is a measure of how much angles between geo directions get expanded or contracted during map projection.
  • GeoGridDirectionDifference[proj,loc,αβ] computes the difference angle (-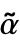)-(β-α) where α, β are azimuths defined on the Earth at the given location loc, and 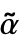, 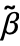are the respective projected bearings on the map.
  • GeoGridDirectionDifference[proj,loc,α] is equivalent to GeoGridDirectionDifference[proj,loc,0α].
  • GeoGridDirectionDifference[proj,loc] computes the largest absolute value of GeoGridDirectionDifference[proj,loc,αα+90] for any value of α.
  • A geo projection can be given as a named projection "proj" with default parameters or as {"proj",params}, where "proj" is any of the entities of GeoProjectionData and params are parameter rules like "StandardParallels"->{33,60}. GeoProjectionData["proj"] gives the default values of the parameters for the projection "proj".
  • The location loc can be given as a coordinate pair {lat,lon} in degrees, a geo position object like GeoPosition[…] or GeoGridPosition[…] or as a geo entity Entity[…].
  • The bearing or azimuthal direction α is an angle measured clockwise from true north. It can be given as a Quantity angle, as a number in degrees or as a named compass direction like "North", "NE" or "NEbE".
  • GeoGridDirectionDifference threads over its location and direction arguments.
  • Possible options of GeoGridDirectionDifference include:
  • GeoModel Automaticmodel of Earth or a celestial body

Examples

open allclose all

Basic Examples  (1)

Compute the angular difference induced by the Mollweide projection in the eastward direction at New York:

The angle between the projected north and east directions is about 27.7° smaller than the original 90°:

Scope  (9)

Compute the geo grid direction difference along the northeast direction for a geo projection at your current geo location:

These are the default values of the parameters of the "Albers" projection:

Specify other values for the parameters of the projection:

Compare any two initial directions with their projected versions:

Specify the azimuth as a number of degrees:

Specify the azimuth as a Quantity angle:

Use any other angular unit:

Specify a location using a pair {lat,lon} in degrees:

Use locations with geo position heads:

Specify a location using a geo Entity object:

Compute the geo grid direction difference for a list of different azimuths at the same location:

The input can also be given as a QuantityArray object:

Find the maximum absolute value of the angular difference of perpendicular directions:

Check the result graphically:

Return the projected angular difference of a list of locations in different formats:

GeoGridDirectionDifference can efficiently process values for large numbers of locations:

Options  (1)

GeoModel  (1)

By default, GeoGridDirectionDifference returns values for a spherical geo model:

Using an ellipsoidal model of Earth produces a slightly different value:

The global scale of the reference model does not affect geo direction distortion:

Properties & Relations  (6)

The geo grid direction difference varies periodically with the azimuth, with a period of 180 degrees:

Compute the azimuths of the minimal and maximal geo grid direction differences:

Compute the maximum value of the geo grid direction difference for perpendicular directions:

Check explicitly that the values agree when you compute them numerically:

Take the cylindrical projections, except for those requiring additional parameters or not given in normal aspect:

Choose 100 random geo locations:

Check that cylindrical projections do not distort the perpendicularity of the north and east directions:

Take the conformal projections, except for those requiring additional parameters:

Choose 100 random geo locations:

Check that the geo grid direction difference is zero at all the chosen points:

Flat polar projections have maximal geo grid angle difference at the poles if the azimuths define a meridian:

Possible Issues  (1)

If a geo location cannot be projected, then the geo grid direction difference cannot be computed either:

This location is not on the half-Earth covered by the "Orthographic" projection with default center:

Neat Examples  (1)

Make a density plot of angular distortion along the eastward direction for the island of Madagascar:

Wolfram Research (2019), GeoGridDirectionDifference, Wolfram Language function, https://reference.wolfram.com/language/ref/GeoGridDirectionDifference.html.

Text

Wolfram Research (2019), GeoGridDirectionDifference, Wolfram Language function, https://reference.wolfram.com/language/ref/GeoGridDirectionDifference.html.

CMS

Wolfram Language. 2019. "GeoGridDirectionDifference." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GeoGridDirectionDifference.html.

APA

Wolfram Language. (2019). GeoGridDirectionDifference. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeoGridDirectionDifference.html

BibTeX

@misc{reference.wolfram_2025_geogriddirectiondifference, author="Wolfram Research", title="{GeoGridDirectionDifference}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/GeoGridDirectionDifference.html}", note=[Accessed: 01-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_geogriddirectiondifference, organization={Wolfram Research}, title={GeoGridDirectionDifference}, year={2019}, url={https://reference.wolfram.com/language/ref/GeoGridDirectionDifference.html}, note=[Accessed: 01-July-2025 ]}