GeometricBrownianMotionProcess
GeometricBrownianMotionProcess[μ,σ,x0]
ドリフトμ,ボラティリティσ,初期値 x0の幾何ブラウン(Brown)運動過程を表す.
詳細

- GeometricBrownianMotionProcessは指数ブラウン運動およびRendleman–Bartterモデルとしても知られている.
- 金融工学では,GeometricBrownianMotionProcessはブラック・ショールズ(Black–Scholes) モデルで株価のモデル化のために使われている.
- GeometricBrownianMotionProcessは連続時間・連続状態のランダム過程である.
- 幾何ブラウン運動の状態
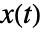 は伊藤微分方程式
は伊藤微分方程式 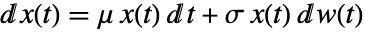 を満足する.ただし,
を満足する.ただし,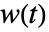 は標準WienerProcess[]に従う.
は標準WienerProcess[]に従う. - 状態
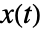 は,LogNormalDistribution[(μ-
は,LogNormalDistribution[(μ-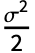 ) t+Log[x0],σ
) t+Log[x0],σ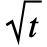 ]に従う.
]に従う. - 母数 μ は任意の実数でよく,σ および x0は任意の正の実数でよい.
- GeometricBrownianMotionProcessは,Mean,PDF,Probability,RandomFunction等の関数で使うことができる.
例題
すべて開くすべて閉じるスコープ (13)
基本的な用法 (8)
過程スライス特性 (5)
一変量時間スライスはLogNormalDistributionに従う:
複数の時間スライスはLogMultinormalDistributionに従う:
CentralMomentは,記号次数について閉形式を持たない:
FactorialMomentは,記号次数について閉形式を持たない:
Cumulantは,記号次数について閉形式を持たない:
一般化と拡張 (1)
アプリケーション (2)
特性と関係 (6)
GeometricBrownianMotionProcessは弱定常ではない:
幾何ブラウン運動過程は特殊なItoProcessである:
特殊なStratonovichProcessでもある:
WienerProcessを直接使ってGeometricBrownianMotionProcessのシミュレーションを行うことができる:
これは,対応するGeometricBrownianMotionProcessのシミュレーションのためのアルゴリズムと一致する:
テキスト
Wolfram Research (2012), GeometricBrownianMotionProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/GeometricBrownianMotionProcess.html (2017年に更新).
CMS
Wolfram Language. 2012. "GeometricBrownianMotionProcess." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/GeometricBrownianMotionProcess.html.
APA
Wolfram Language. (2012). GeometricBrownianMotionProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeometricBrownianMotionProcess.html