GeometricBrownianMotionProcess
GeometricBrownianMotionProcess[μ,σ,x0]
表示几何布朗运动过程,其中漂移量为 μ,波动率为 σ,初始值为 x0.
更多信息

- GeometricBrownianMotionProcess 亦称为指数布朗运动和 Rendleman–Bartter 模型.
- 在数学金融学中,GeometricBrownianMotionProcess 被用在模拟股票价格的 Black–Scholes 模型中.
- GeometricBrownianMotionProcess 是一个连续时间和连续状态随机过程.
- 几何布朗运动的状态
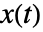 满足伊藤微分方程
满足伊藤微分方程 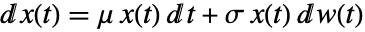 ,其中
,其中 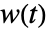 服从标准WienerProcess[].
服从标准WienerProcess[]. - 状态
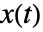 服从 LogNormalDistribution[(μ-
服从 LogNormalDistribution[(μ-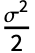 ) t+Log[x0],σ
) t+Log[x0],σ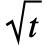 ].
]. - 参数 μ 可以是任意实数,而 σ 和 x0 是任意正实数.
- GeometricBrownianMotionProcess 可以与诸如 Mean、PDF、Probability 和 RandomFunction 等函数一起使用.
范例
打开所有单元关闭所有单元范围 (13)
过程切片性质 (5)
单变量时间切片服从 LogNormalDistribution:
多时间切片服从 LogMultinormalDistribution:
在符号式阶数下,CentralMoment 没有解析形式:
在符号式阶数下,FactorialMoment 没有解析形式:
在符号式阶数下,Cumulant 没有解析形式:
推广和延伸 (1)
应用 (2)
属性和关系 (6)
GeometricBrownianMotionProcess 不是弱平稳过程:
几何布朗运动过程是一个特殊的 ItoProcess:
使用 WienerProcess 直接模拟 GeometricBrownianMotionProcess:
它与模拟相应的 GeometricBrownianMotionProcess 算法一致:
文本
Wolfram Research (2012),GeometricBrownianMotionProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/GeometricBrownianMotionProcess.html (更新于 2017 年).
CMS
Wolfram 语言. 2012. "GeometricBrownianMotionProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/GeometricBrownianMotionProcess.html.
APA
Wolfram 语言. (2012). GeometricBrownianMotionProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GeometricBrownianMotionProcess.html 年