GoldenRatio

GoldenRatio

黄金比 で，この数値はとなる．

詳細

  • NumericQには数値として，Dには定数として扱われる数学定数である．
  • GoldenRatioは，Nを使って任意の数値精度で評価することができる．

予備知識

  • GoldenRatioは，黄金比 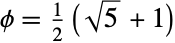を表すシンボル，連続するフィボナッチ数の比の極限値 lim_(n->infty) (TemplateBox[{n}, Fibonacci])/(TemplateBox[{{n, -, 1}}, Fibonacci])を与える定数，可能な中で「最も単純」な連分数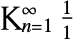の値である．その値は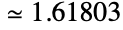である．GoldenRatioは，総和，再帰関係，連分数，ネストした累乗根，特別な三角関数の値，五角形，星形五角形，十二角形等の単純な幾何学的図形の辺の長さの比等，数多くの数学計算に見られる．GoldenRatioは，数多くの自然現象や対数螺線にも関連している．
  • GoldenRatioがシンボルとして用いられた場合は，FunctionExpandを使って累乗根として表現できる厳密な数量として伝播される．GoldenRatioを含む複雑な式の展開と簡約には，FunctionExpandやFullSimplify等の関数が必要なことがある．
  • GoldenRatioは，その代数定義によると，無理数（2つの整数の比としては表すことができない）であるが，代数的（整数多項式，この場合は 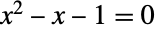，の根）である．GoldenRatioが，どんな底についても正規数である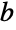（ を底とした各桁の数字の展開が一様に分布している）かどうかは不明であるが，既知の各桁の数字は非常に一様に分布している．
  • GoldenRatioはNを使って任意の数値精度に評価することができる．実際，最新のデスクトップコンピュータを使ったGoldenRatioの最初の百万桁の計算には，1秒の数分の一しかかからない．RealDigitsを使ってGoldenRatioの各桁の数字のリストを返すことができ，ContinuedFractionを使ってその連分数展開の項のリストを得ることができる．

例題

すべて開くすべて閉じる

例  (1)

数値：

スコープ  (4)

任意精度で評価する：

厳密計算を行う：

GoldenRatioの式を簡約する：

TraditionalFormによる表示：

アプリケーション  (7)

黄金比の長方形：

葉序パターン（ひまわりのシミュレーション）を作る：

フィボナッチ数を計算する：

正20面体の角：

フィボナッチの代入システムにおける1の位置 [詳細]：

フィボナッチ数の有効な「逆」数を計算する：

特性と関係  (3)

おもしろい例題  (1)

ヤシの木の幹のシミュレーション：

Wolfram Research (1988), GoldenRatio, Wolfram言語関数， https://reference.wolfram.com/language/ref/GoldenRatio.html.

テキスト

Wolfram Research (1988), GoldenRatio, Wolfram言語関数， https://reference.wolfram.com/language/ref/GoldenRatio.html.

CMS

Wolfram Language. 1988. "GoldenRatio." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GoldenRatio.html.

APA

Wolfram Language. (1988). GoldenRatio. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GoldenRatio.html

BibTeX

@misc{reference.wolfram_2024_goldenratio, author="Wolfram Research", title="{GoldenRatio}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/GoldenRatio.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_goldenratio, organization={Wolfram Research}, title={GoldenRatio}, year={1988}, url={https://reference.wolfram.com/language/ref/GoldenRatio.html}, note=[Accessed: 22-November-2024 ]}