WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

Fibonacci
✖
Fibonacci

✖

gives the Fibonacci number .

✖
Fibonacci[n,x]

gives the Fibonacci polynomial .

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • The 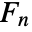satisfy the recurrence relation 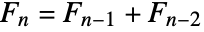with .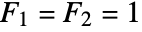
  • For any complex value of n, the 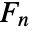are given by the general formula 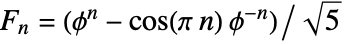, where 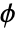is the golden ratio.
  • The Fibonacci polynomial 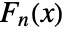is the coefficient of 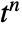in the expansion of .
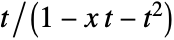  • The Fibonacci polynomials satisfy the recurrence relation .
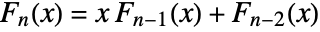  • FullSimplify and FunctionExpand include transformation rules for combinations of Fibonacci numbers with symbolic arguments when the arguments are specified to be integers using n∈Integers.
  • Fibonacci can be evaluated to arbitrary numerical precision.
  • Fibonacci automatically threads over lists.
  • Fibonacci can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (6)Summary of the most common use cases

Compute Fibonacci numbers:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-on9
Out[1]=1

Plot over a subset of the reals:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-bi2uyi
Out[1]=1

Plot over a subset of the complexes:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-kiedlx
Out[1]=1

Series expansion at the origin:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-d4yi7q
Out[1]=1

Series expansion at Infinity:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-cugjvu
Out[1]=1

Series expansion at a singular point:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-iffsoc
Out[1]=1

Scope  (43)Survey of the scope of standard use cases

Numerical Evaluation  (6)

Evaluate numerically:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-l274ju
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-cksbl4
Out[2]=2

Evaluate to high precision:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-b0wt9
Out[1]=1

The precision of the output tracks the precision of the input:

In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-y7k4a
Out[2]=2

Complex number inputs:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-hfml09
Out[1]=1

Evaluate efficiently at high precision:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-di5gcr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-bq2c6r
Out[2]=2

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-h0d6g
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-dj6d9x
Out[2]=2

Or compute average-case statistical intervals using Around:

In[3]:=3
✖
https://wolfram.com/xid/0wggrdg-cw18bq
Out[3]=3

Compute the elementwise values of an array:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-thgd2
Out[1]=1

Or compute the matrix Fibonacci function using MatrixFunction:

In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-o5jpo
Out[2]=2

Specific Values  (6)

Values of Fibonacci at fixed points:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-nww7l
Out[1]=1

Fibonacci polynomial for symbolic n and x:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-fc9m8o
Out[1]=1

Values at zero:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-bmqd0y
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-e41pf2
Out[2]=2

Find the value of in which TemplateBox[{3, x}, Fibonacci2]=5:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-f2hrld
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-n57vp9
Out[2]=2

Compute the Fibonacci[7,x] polynomial:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-klij8s
Out[1]=1

Compute Fibonacci[1/2,x]:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-hfz8z6
Out[1]=1

Visualization  (5)

Plot the Fibonacci function:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-ep4mxd
Out[1]=1

Plot the Fibonacci polynomial for various orders:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-ecj8m7
Out[1]=1

Plot the real part of TemplateBox[{3, z}, Fibonacci2]:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-b9zx
Out[1]=1

Plot the imaginary part of TemplateBox[{3, z}, Fibonacci2]:

In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-h9nohr
Out[2]=2

Plot as real parts of two parameters vary:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-elqrq8
Out[1]=1

Types 2 and 3 of Fibonacci polynomial have different branch cut structures:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-dum9su
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-dgvzwe
Out[2]=2

Function Properties  (14)

Fibonacci is defined for all real values:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-cl7ele
Out[1]=1

Approximate function range of Fibonacci:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-evf2yr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-fphbrc
Out[2]=2

Fibonacci polynomial of an even order is odd:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-dnla5q
Out[1]=1

Fibonacci polynomial of an odd order is even:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-bi1e9n
Out[1]=1

Fibonacci has the mirror property TemplateBox[{n}, Fibonacci](z)=TemplateBox[{n}, Fibonacci](z):

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-heoddu
Out[1]=1

Fibonacci threads elementwise over lists:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-svc
Out[1]=1

Fibonacci is an analytic function of x:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-d4cd2p
Out[1]=1

Fibonacci is neither non-decreasing nor non-increasingfor odd values:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-hkxwdp
Out[1]=1

Fibonacci is non-decreasing for even values:

In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-g6kynf
Out[2]=2

Fibonacci is not injective for odd values:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-fxi9f9
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-zf7zy
Out[2]=2

Fibonacci is not surjective for odd values:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-laaoku
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-c5tkuy
Out[2]=2

Fibonacci is non-negative for odd values:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-fxktl8
Out[1]=1

Fibonacci has no singularities or discontinuities:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-qfcpy6
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-bfc30u
Out[2]=2

Fibonacci is convex for odd values:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-duxck
Out[1]=1

TraditionalForm formatting:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-kiuxyj

Differentiation  (3)

First derivatives with respect to n:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-krpoah
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-dd1jfo
Out[2]=2

First derivative with respect to x:

In[3]:=3
✖
https://wolfram.com/xid/0wggrdg-ez6occ
Out[3]=3

Higher derivatives with respect to n:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-z33jv
Out[1]=1

Plot the higher derivatives with respect to n:

In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-fxwmfc
Out[2]=2

Formula for the ^(th) derivative with respect to n:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-cb5zgj
Out[1]=1

Integration  (3)

Compute the indefinite integral using Integrate:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-bponid
Out[1]=1

Definite integral:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-b9jw7l
Out[1]=1

More integrals:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-cas
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-76sc
Out[2]=2

Series Expansions  (4)

Find the Taylor expansion using Series:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-ewr1h8
Out[1]=1

Plots of the first three approximations around :

In[3]:=3
✖
https://wolfram.com/xid/0wggrdg-binhar
Out[4]=4

General term in the series expansion using SeriesCoefficient:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-dznx2j
Out[1]=1

Find the series expansion at Infinity:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-syq
Out[1]=1

Taylor expansion at a generic point:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-jwxla7
Out[1]=1

Function Identities and Simplifications  (2)

The ordinary generating function of Fibonacci:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-j2oret
Out[1]=1

Recurrence relation:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-cq178j
Out[1]=1

Generalizations & Extensions  (2)Generalized and extended use cases

Fibonacci polynomials:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-s4l
Out[1]=1

General series expansion at infinity:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-jhq
Out[1]=1

Applications  (13)Sample problems that can be solved with this function

Solve the Fibonacci recurrence equation:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-jhwy4x
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-bbu2xl
Out[2]=2

Solve another Fibonacci recurrence equation:

In[3]:=3
✖
https://wolfram.com/xid/0wggrdg-h7f
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0wggrdg-y9f
Out[4]=4

Find ratios of successive Fibonacci numbers:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-bhp
Out[1]=1

Compare with continued fractions:

In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-ttp
Out[2]=2

Convergence to the golden ratio:

In[3]:=3
✖
https://wolfram.com/xid/0wggrdg-fk1
Out[3]=3

Fibonacci substitution system:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-0d
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-sup
Out[2]=2

Fibonomial coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-6j
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-f6o
Out[2]=2

Calculate the number of ways to write an integer as a sum of Fibonacci numbers :

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-xbv

Plot the counts for the first hundred integers:

In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-bnncvi
Out[2]=2

Lamé's theorem bounds the number of steps of the Euclidean algorithm for calculating :

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-emi
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-iy4

Plot the maximal number of steps:

In[3]:=3
✖
https://wolfram.com/xid/0wggrdg-gkq
Out[3]=3

Find the first Fibonacci number above 1000000:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-v0e
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-e870i
Out[2]=2

Plot the discrete inverse of Fibonacci numbers:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-tqt
Out[1]=1

Plot of the absolute value of Fibonacci over the complex plane:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-kt3
Out[1]=1

Find the number of factors of Fibonacci polynomials:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-zi
Out[1]=1

If divides TemplateBox[{m}, Fibonacci], then TemplateBox[{n}, Fibonacci] divides TemplateBox[{TemplateBox[{m}, Fibonacci]}, Fibonacci]:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-dit7gz
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-kxsa0
In[3]:=3
✖
https://wolfram.com/xid/0wggrdg-474fx
Out[3]=3

This is a particular case of a more general identity gcd(TemplateBox[{n}, Fibonacci],TemplateBox[{k}, Fibonacci])=TemplateBox[{{gcd, (, {n, ,, k}, )}}, Fibonacci]:

In[4]:=4
✖
https://wolfram.com/xid/0wggrdg-c6337o
Out[4]=4

The sequence of TemplateBox[{TemplateBox[{n}, Fibonacci], m}, Mod] is periodic with respect to for a fixed natural number :

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-b1kjg1
Out[1]=1

For , the period equals :

In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-ezv2ym
Out[2]=2

Build Zeckendorf's representation of a positive integer [MathWorld]:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-cya1fa
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-giaizb
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0wggrdg-b7nshg
Out[3]=3

Define Fibonacci multiplication for positive integers:

In[4]:=4
✖
https://wolfram.com/xid/0wggrdg-2ycp2

Fibonacci multiplication table:

In[5]:=5
✖
https://wolfram.com/xid/0wggrdg-ewghza
Out[5]=5

Verify that the Fibonacci multiplication is associative:

In[6]:=6
✖
https://wolfram.com/xid/0wggrdg-ckqpj8
Out[6]=6

Properties & Relations  (15)Properties of the function, and connections to other functions

Fibonacci Numbers  (13)

Expand in terms of elementary functions:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-eqx
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-rt2
Out[2]=2

Limiting ratio:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-pxq
Out[1]=1

Explicit recursive definition:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-mnv
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-1u
In[3]:=3
✖
https://wolfram.com/xid/0wggrdg-zgn
Out[3]=3

Explicit state‐space recursive definition:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-j57xh
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-b20glg
In[3]:=3
✖
https://wolfram.com/xid/0wggrdg-cb96j6
In[4]:=4
✖
https://wolfram.com/xid/0wggrdg-kn0oqw
Out[4]=4

Closed‐form solution using MatrixPower:

In[5]:=5
✖
https://wolfram.com/xid/0wggrdg-fwu5wy
Out[5]=5

Simplify expressions involving Fibonacci numbers:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-po7
Out[1]=1

Symbolic summation:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-qhl
Out[1]=1

Generating function:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-vzs
Out[1]=1

Fibonacci numbers as coefficients:

In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-zcw
Out[2]=2

Express a fractional Fibonacci number as an algebraic number:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-pzo
Out[1]=1

Fibonacci can be represented as a DifferenceRoot:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-pxkma
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-53182
Out[2]=2

General term in the series expansion of Fibonacci:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-dlm2b6
Out[1]=1

The generating function for Fibonacci:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-pz93yz
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-frz0l8
Out[2]=2

FindSequenceFunction can recognize the Fibonacci sequence:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-hj2mn6
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-5okec
Out[2]=2

The exponential generating function for Fibonacci:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-gaiyeu
Out[1]=1

Fibonacci Polynomials  (2)

Expand in terms of elementary functions:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-b10
Out[1]=1

Explicitly construct Fibonacci polynomials:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-ic1g
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-yc4
Out[2]=2

Possible Issues  (3)Common pitfalls and unexpected behavior

Large arguments can give results too large to be computed explicitly:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-v3y
Out[1]=1

Results for integer arguments may not hold for non-integers:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-emc
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-er4
Out[2]=2

Matrix power representation is valid only for integers:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-hnc
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-zcb
Out[2]=2

Neat Examples  (8)Surprising or curious use cases

Fibonacci numbers modulo 10:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-qpr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-hae
Out[2]=2

Fibonacci modulo n [more info]:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-bx9
Out[1]=1

Count the number of 1, 2, ..., 9, 0 digits in the 1,000,000^(th) Fibonacci number:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-b99v9u
Out[1]=1

Contours of vanishing real and imaginary parts of Fibonacci:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-h1k5c5
Out[1]=1

LogPlot of positive and negative Fibonacci numbers:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-ig2h1a
Out[1]=1

While the Fibonacci numbers are nondecreasing for non-negative arguments, the Fibonacci function possesses a single local minimum:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-gqu
Out[1]=1

Since the generating function is rational, these sums come out as rational numbers:

In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-qd3cak
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0wggrdg-st0
Out[2]=2
In[1]:=1
✖
https://wolfram.com/xid/0wggrdg-nlg
Out[1]=1
Wolfram Research (1996), Fibonacci, Wolfram Language function, https://reference.wolfram.com/language/ref/Fibonacci.html (updated 2002).
✖
Wolfram Research (1996), Fibonacci, Wolfram Language function, https://reference.wolfram.com/language/ref/Fibonacci.html (updated 2002).

Text

Wolfram Research (1996), Fibonacci, Wolfram Language function, https://reference.wolfram.com/language/ref/Fibonacci.html (updated 2002).

✖
Wolfram Research (1996), Fibonacci, Wolfram Language function, https://reference.wolfram.com/language/ref/Fibonacci.html (updated 2002).

CMS

Wolfram Language. 1996. "Fibonacci." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2002. https://reference.wolfram.com/language/ref/Fibonacci.html.

✖
Wolfram Language. 1996. "Fibonacci." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2002. https://reference.wolfram.com/language/ref/Fibonacci.html.

APA

Wolfram Language. (1996). Fibonacci. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Fibonacci.html

✖
Wolfram Language. (1996). Fibonacci. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Fibonacci.html

BibTeX

@misc{reference.wolfram_2025_fibonacci, author="Wolfram Research", title="{Fibonacci}", year="2002", howpublished="\url{https://reference.wolfram.com/language/ref/Fibonacci.html}", note=[Accessed: 29-March-2025 ]}

✖
@misc{reference.wolfram_2025_fibonacci, author="Wolfram Research", title="{Fibonacci}", year="2002", howpublished="\url{https://reference.wolfram.com/language/ref/Fibonacci.html}", note=[Accessed: 29-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_fibonacci, organization={Wolfram Research}, title={Fibonacci}, year={2002}, url={https://reference.wolfram.com/language/ref/Fibonacci.html}, note=[Accessed: 29-March-2025 ]}

✖
@online{reference.wolfram_2025_fibonacci, organization={Wolfram Research}, title={Fibonacci}, year={2002}, url={https://reference.wolfram.com/language/ref/Fibonacci.html}, note=[Accessed: 29-March-2025 ]}