GoldenRatio （黄金比例）

GoldenRatio

给出黄金比率 ，其数值 .

更多信息

  • 数学常数，NumericQ 将其视为数值，D 将其视为常数.
  • GoldenRatio 使用 N 可以计算到任意数值精度.

背景

  • GoldenRatio 是表示黄金比例 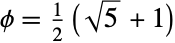的符号. 这一常数给出了相邻斐波那契数之比 lim_(n->infty) (TemplateBox[{n}, Fibonacci])/(TemplateBox[{{n, -, 1}}, Fibonacci]) 的极限值，同时也是“最简单”的连分数 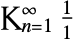的值. 它的数值 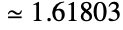. GoldenRatio 出现在许多数学计算中，包括求和、递推关系、连分数、多重根式、特殊三角函数值以及像五边形、五角星和正十二面体这样的简单几何图形的边长比例. 和对数螺旋线一样， GoldenRatio 还和许多自然出现的现象有关联.
  • 当 GoldenRatio 作为符号时，它被当成精确值参与计算，并可用 FunctionExpand 表示成根式的形式. 展开及化简一些复杂的含有 GoldenRatio 的表达式可能要用到如 FunctionExpand 和 FullSimplify 这样的函数.
  • 基于其代数上的定义，GoldenRatio 是无理数（这意味着它不能被表示成任意一对整数的比值）也是代数数（这意味着它是某个整数系数多项式的根—这里这个多项式方程是 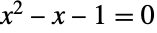）. 尽管现在还不知道 GoldenRatio 是否是某个进位制下的正规数（这意味着它在 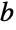进制下的各位数字均匀分布），但它已知的各位数字分布得还是很均匀的.
  • 用 N 可以算出 GoldenRatio 的任意精度的数值. 事实上在一台现代台式电脑上计算 GoldenRatio 的前一百万位数字耗时都不到一秒. RealDigits 可用于返回 GoldenRatio 的各位数字列表而 ContinuedFraction 则可得到其连分数展开的各项.

范例

打开所有单元关闭所有单元

基本范例  (1)

数值结果：

范围  (4)

任意精度的计算：

执行精确的计算：

化简 GoldenRatio 表达式：

TraditionalForm 格式：

应用  (7)

黄金比率的矩形：

制作一个叶序模式 (“模仿向日葵”)：

计算斐波那契数：

一个二十面体的角：

在一个斐波那契替代系统中 1 的位置 [更多信息]：

计算斐波那契数的有效“逆”：

属性和关系  (3)

巧妙范例  (1)

模仿棕榈树的树干：

Wolfram Research (1988)，GoldenRatio （黄金比例），Wolfram 语言函数，https://reference.wolfram.com/language/ref/GoldenRatio.html.

文本

Wolfram Research (1988)，GoldenRatio （黄金比例），Wolfram 语言函数，https://reference.wolfram.com/language/ref/GoldenRatio.html.

CMS

Wolfram 语言. 1988. "GoldenRatio （黄金比例）." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/GoldenRatio.html.

APA

Wolfram 语言. (1988). GoldenRatio （黄金比例）. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GoldenRatio.html 年

BibTeX

@misc{reference.wolfram_2024_goldenratio （黄金比例）, author="Wolfram Research", title="{GoldenRatio （黄金比例）}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/GoldenRatio.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_goldenratio （黄金比例）, organization={Wolfram Research}, title={GoldenRatio （黄金比例）}, year={1988}, url={https://reference.wolfram.com/language/ref/GoldenRatio.html}, note=[Accessed: 22-November-2024 ]}